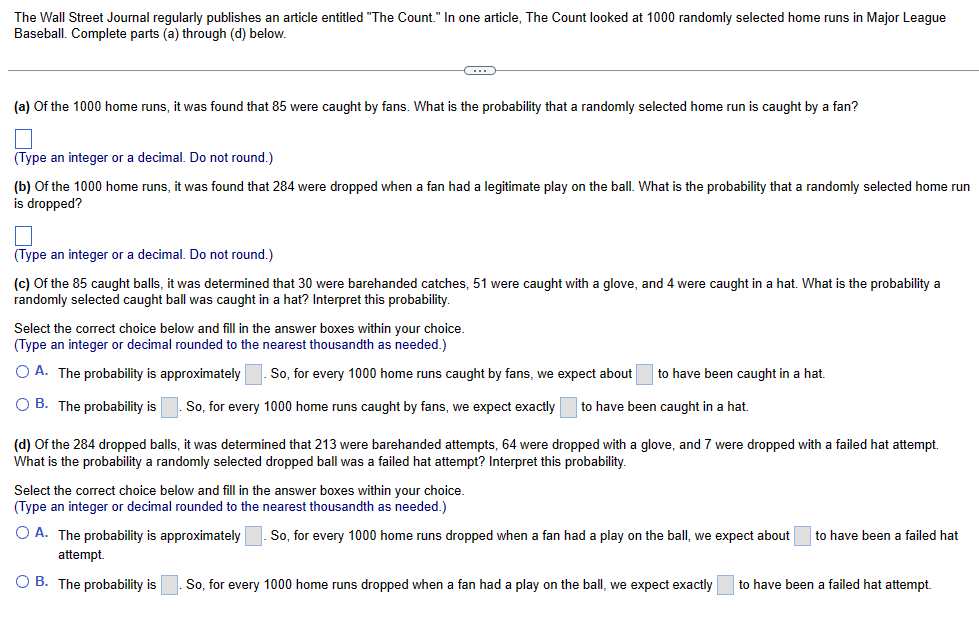
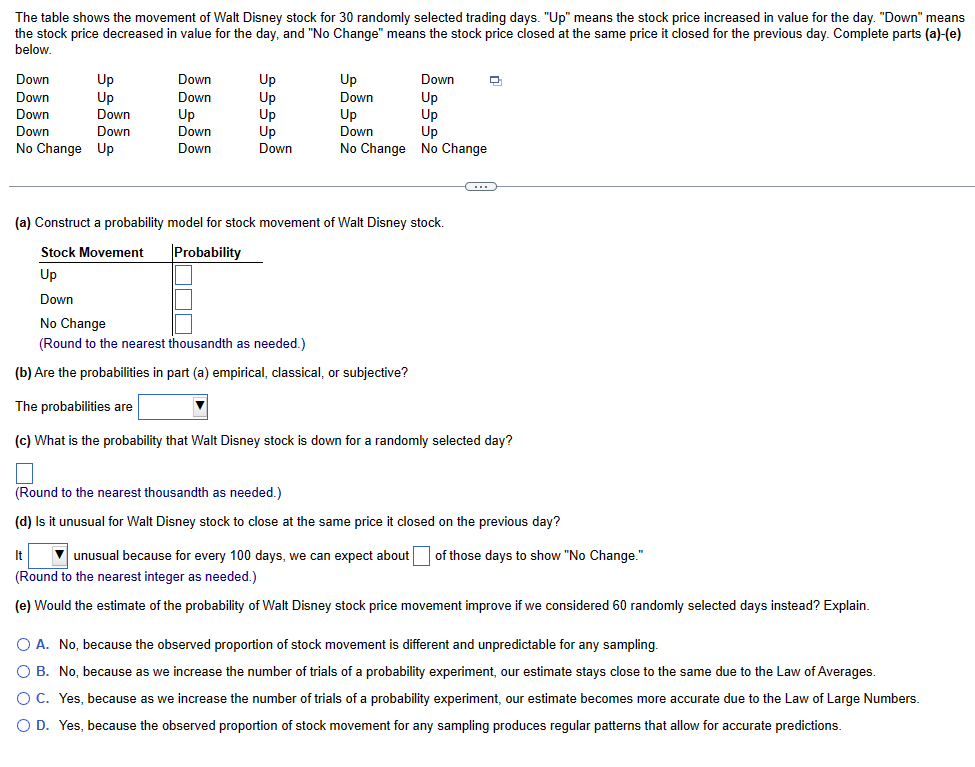
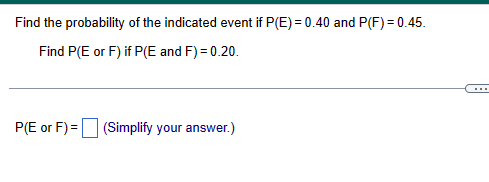
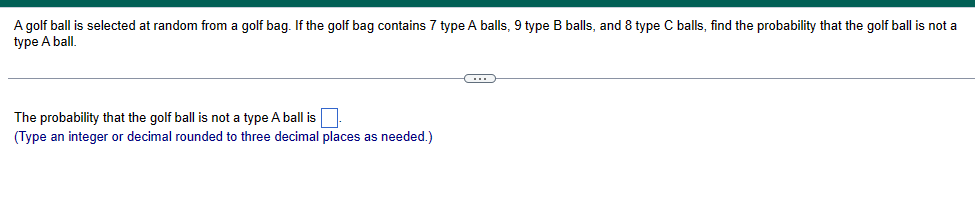
The Wall Street Journal regularly publishes an article entitled "The Count." In one article, The Count looked at 1000 randomly selected home runs in Major League Baseball. Complete parts (a) through (d) below. (a) Of the 1000 home runs, it was found that 85 were caught by fans. What is the probability that a randomly selected home run is caught by a fan? (Type an integer or a decimal. Do not round.) (b) Of the 1000 home runs, it was found that 284 were dropped when a fan had a legitimate play on the ball. What is the probability that a randomly selected home run is dropped? (Type an integer or a decimal. Do not round.) (c) Of the 85 caught balls, it was determined that 30 were barehanded catches, 51 were caught with a glove, and 4 were caught in a hat. What is the probability a randomly selected caught ball was caught in a hat? Interpret this probability. Select the correct choice below and fill in the answer boxes within your choice. (Type an integer or decimal rounded to the nearest thousandth as needed.) A. The probability is approximately OB. The probability is So, for every 1000 home runs caught by fans, we expect about to have been caught in a hat. So, for every 1000 home runs caught by fans, we expect exactly to have been caught in a hat. (d) of the 284 dropped balls, it was determined that 213 were barehanded attempts, 64 were dropped with a glove, and 7 were dropped with a failed hat attempt. What is the probability a randomly selected dropped ball was a failed hat attempt? Interpret this probability. Select the correct choice below and fill in the answer boxes within your choice. (Type an integer or decimal rounded to the nearest thousandth as needed.) OA. The probability is approximately attempt. OB. The probability is . So, for every 1000 home runs dropped when a fan had a play on the ball, we expect about to have been a failed hat So, for every 1000 home runs dropped when a fan had a play on the ball, we expect exactly to have been a failed hat attempt. The table shows the movement of Walt Disney stock for 30 randomly selected trading days. "Up" means the stock price increased in value for the day. "Down" means the stock price decreased in value for the day, and "No Change" means the stock price closed at the same price it closed for the previous day. Complete parts (a)-(e) below. Down Up Down Up Up Down Down Up Down Up Down Up Down Down Up Up Up Up Down Down Down Up Down Up No Change Up Down Down No Change No Change (a) Construct a probability model for stock movement of Walt Disney stock. Stock Movement Probability Up Down No Change (Round to the nearest thousandth as needed.) (b) Are the probabilities in part (a) empirical, classical, or subjective? The probabilities are (c) What is the probability that Walt Disney stock is down for a randomly selected day? (Round to the nearest thousandth as needed.) (d) Is it unusual for Walt Disney stock to close at the same price it closed on the previous day? It unusual because for every 100 days, we can expect about of those days to show "No Change." (Round to the nearest integer as needed.) (e) Would the estimate of the probability of Walt Disney stock price movement improve if we considered 60 randomly selected days instead? Explain. A. No, because the observed proportion of stock movement is different and unpredictable for any sampling. B. No, because as we increase the number of trials of a probability experiment, our estimate stays close to the same due to the Law of Averages. C. Yes, because as we increase the number of trials of a probability experiment, our estimate becomes more accurate due to the Law of Large Numbers. D. Yes, because the observed proportion of stock movement for any sampling produces regular patterns that allow for accurate predictions. Describe what an unusual event is. Should the same cutoff always be used to identify unusual events? Why or why not? Choose the correct answer below. A. An event is unusual if it has a high probability of occurring. The same cutoff should always be used to identify unusual events. An event is unusual regardless of the context of the event. B. An event is unusual if it has a low probability of occurring. The same cutoff should always be used to identify unusual events. An event is unusual regardless of the context of the event. C. An event is unusual if it has a high probability of occurring. The same cutoff should not always be used to identify unusual events. Selecting a cutoff is subjective and should take into account the consequences of incorrectly identifying an event as unusual. D. An event is unusual if it has a low probability of occurring. The same cutoff should not always be used to identify unusual events. Selecting a cutoff is subjective and should take into account the consequences of incorrectly identifying an event as unusual. Describe the difference between classical and empirical probability. Choose the correct answer below. A. The empirical method obtains an exact empirical probability of an event by conducting a probability experiment. The classical method of computing probabilities does not require that a probability experiment actually be performed. Rather, it relies on counting techniques, and requires equally likely outcomes. B. The empirical method obtains an approximate empirical probability of an event by conducting a probability experiment. The classical method of computing probabilities does not require that a probability experiment actually be performed. Rather, it relies on counting techniques, and requires equally likely outcomes. C. The classical method obtains an exact probability of an event by conducting a probability experiment. The empirical method of computing empirical probabilities does not require that a probability experiment actually be performed. Rather, it relies on counting techniques, and requires equally likely outcomes. OD. The classical method obtains an approximate empirical probability of an event by conducting a probability experiment. The empirical method of computing probabilities does not require that a probability experiment actually be performed. Rather, it relies on counting techniques, and requires equally likely outcomes. A probability experiment is conducted in which the sample space of the experiment is S = {3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}, event E = {5, 6, 7, 8, 9} and event G={10, 11, 12, 13}. Assume that each outcome is equally likely. List the outcomes in E and G. Are E and G mutually exclusive? List the outcomes in E and G. Choose the correct answer below. OA. E and G = {} (Use a comma to separate answers as needed.) B. E and G = {} Are E and G mutually exclusive? A. Yes, because the events E and G have no outcomes in common. B. Yes, because the events E and G have at least one outcome in common. OC. No, because the events E and G have outcomes in common. D. No, because the events E and G have at least one outcome in common. Find the probability of the indicated event if P(E)= 0.40 and P(F)= 0.45. Find P(E or F) if P(E and F) = 0.20. P(E or F) = (Simplify your answer.) A golf ball is selected at random from a golf bag. If the golf bag contains 7 type A balls, 9 type B balls, and 8 type C balls, find the probability that the golf ball is not a type A ball. The probability that the golf ball is not a type A ball is (Type an integer or decimal rounded to three decimal places as needed.) A university conducted a survey of 385 undergraduate students regarding satisfaction with student government. Results of the survey are shown in the table by class rank. Complete parts (a) through (d) below. Click the icon to view the table. (a) If a survey participant is selected at random, what is the probability that he or she is satisfied with student government? P(satisfied) = (Round to three decimal places as needed.) (b) If a survey participant is selected at random, what is the probability that he or she is a junior? P(junior) = (Round to three decimal places as needed.) (c) If a survey participant is selected at random, what is the probability that he or she is satisfied and a junior? P(satisfied and junior) = (Round to three decimal places as needed.) (d) If a survey participant is selected at random, what is the probability that he or she is satisfied or a junior? P(satisfied or junior) =]] (Round to three decimal places as needed.) What is the probability of obtaining eight heads in a row when flipping a coin? Interpret this probability. The probability of obtaining eight heads in a row when flipping a coin is (Round to five decimal places as needed.) Interpret this probability. Consider the event of a coin being flipped eight times. If that event is repeated ten thousand different times, it is expected that the event would result in eight heads about time(s). (Round to the nearest whole number as needed.) In airline applications, failure of a component can result in catastrophe. As a result, many airline components utilize something called triple modular redundancy. This means that a critical component has two backup components that may be utilized should the initial component fail. Suppose a certain critical airline component has a probability of failure of 0.0064 and the system that utilizes the component is part of a triple modular redundancy. (a) Assuming each component's failure/success is independent of the others, what is the probability all three components fail, resulting in disaster for the flight? (b) What is the probability at least one of the components does not fail? (a) The probability is (Round to eight decimal places as needed.) (b) The probability is (Round to eight decimal places as needed.)