Then it would run this after

Xtrain,ytrain,Xtest,ytest = pickle.load(open('diabetes.pickle','rb'),encoding='latin1')

# add intercept

Xtrain_i = np.concatenate((np.ones((Xtrain.shape[0],1)), Xtrain), axis=1)

Xtest_i = np.concatenate((np.ones((Xtest.shape[0],1)), Xtest), axis=1)

args = (Xtrain_i,ytrain)

opts = {'maxiter' : 50} # Preferred value.

w_init = np.zeros((Xtrain_i.shape[1],1))

soln = minimize(regressionObjVal, w_init, jac=regressionGradient, args=args,method='CG', options=opts)

w = np.transpose(np.array(soln.x))

w = w[:,np.newaxis]

rmse = testOLERegression(w,Xtrain_i,ytrain)

print('Gradient Descent Linear Regression RMSE on train data - %.2f'%rmse)

rmse = testOLERegression(w,Xtest_i,ytest)

print('Gradient Descent Linear Regression RMSE on test data - %.2f'%rmse)

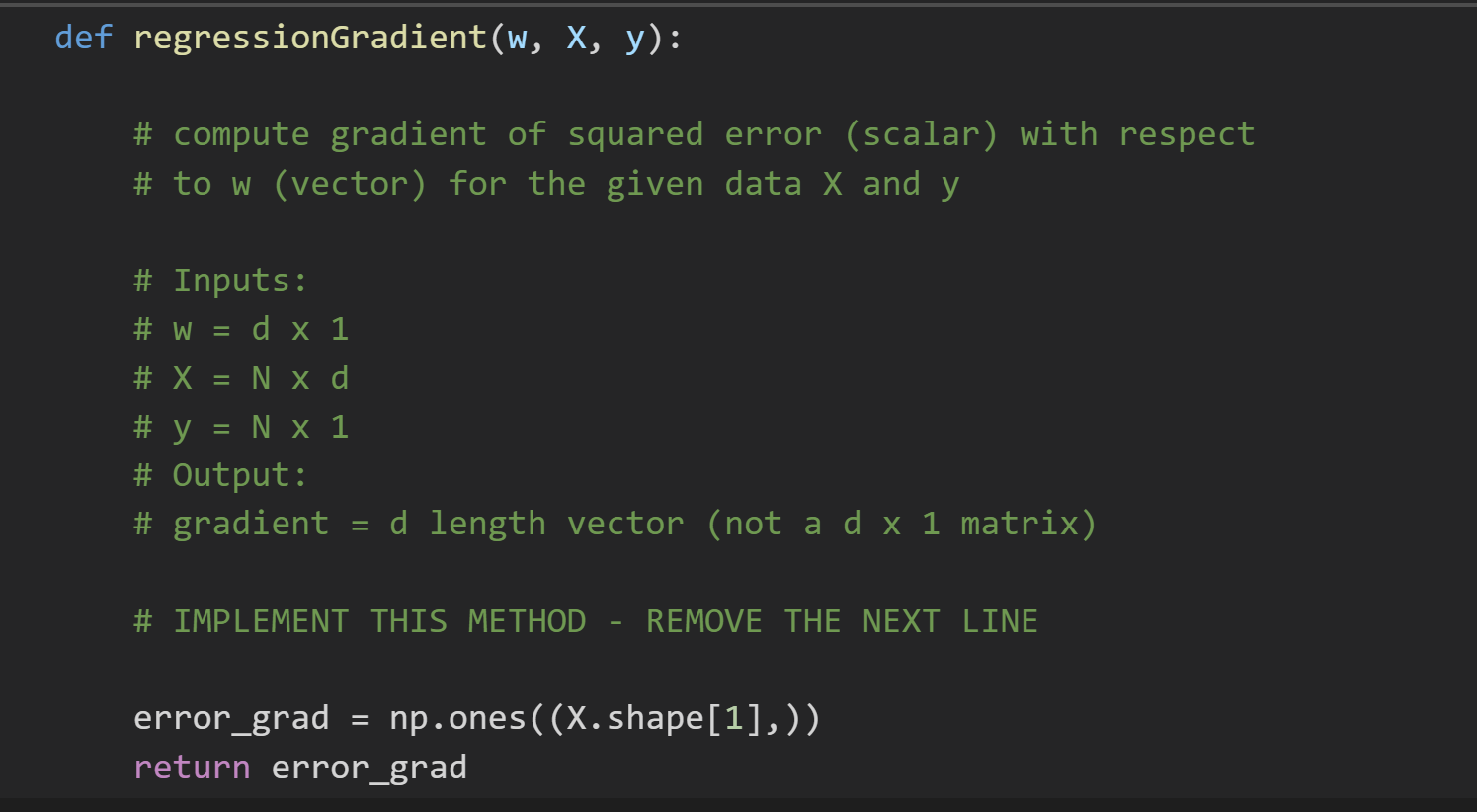
def regressionGradient(W, X, y): # compute gradient of squared error (scalar) with respect # to w (vector) for the given data X and y # Inputs: # W = d x 1 # X = N xd # y = N x 1 # Output: # gradient d length vector (not a d x 1 matrix) # IMPLEMENT THIS METHOD REMOVE THE NEXT LINE error_grad = np.ones((X.shape[1],)) return error_grad