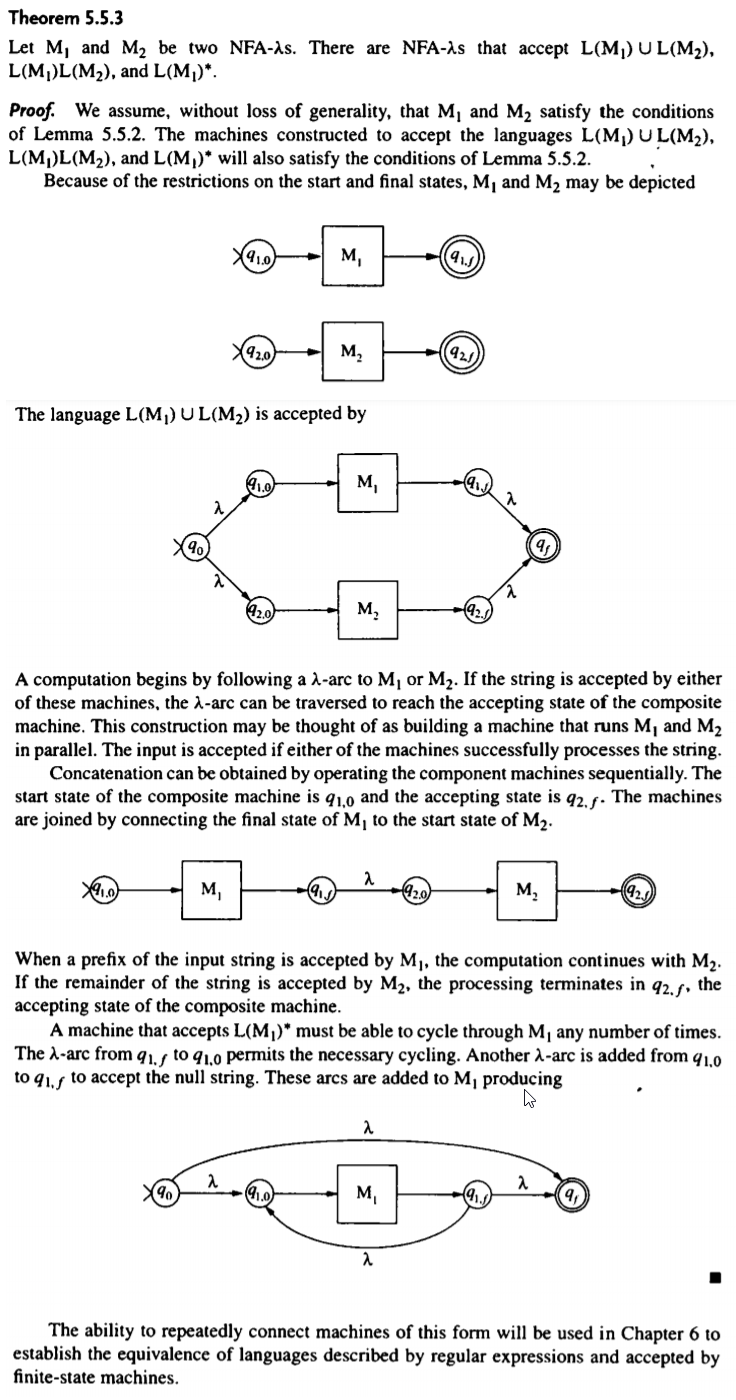
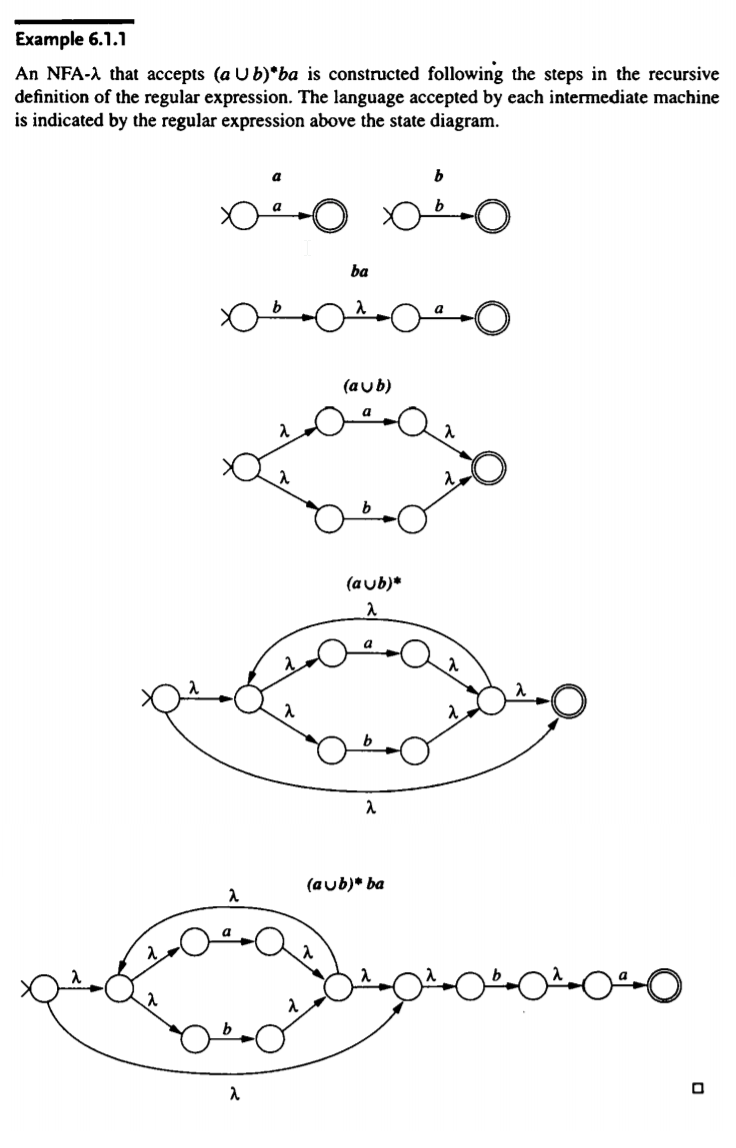
Theorem 5.5.3 Let M, and M2 be two NFA-As. There are NFA as that accept L(M) UL(M2), L(M)L(M2), and L(M)* Proof. We assume, without loss of generality, that M, and M2 satisfy the conditions of Lemma 5.5.2. The machines constructed to accept the languages L(M) UL(M2), L(M)L(M2), and L(M)* will also satisfy the conditions of Lemma 5.5.2. Because of the restrictions on the start and final states, M, and M2 may be depicted 91.0 M, 91 92.0 M 921 The language L(M) UL(M2) is accepted by M 90 M A computation begins by following a l-arc to M, or M2. If the string is accepted by either of these machines, the A-arc can be traversed to reach the accepting state of the composite machine. This construction may be thought of as building a machine that runs M, and M2 in parallel. The input is accepted if either of the machines successfully processes the string. Concatenation can be obtained by operating the component machines sequentially. The start state of the composite machine is 91,0 and the accepting state is 92.g. The machines are joined by connecting the final state of M, to the start state of M2. M M, (92.1 When a prefix of the input string is accepted by My, the computation continues with M2. If the remainder of the string is accepted by M2, the processing terminates in 92.g, the accepting state of the composite machine. A machine that accepts L(M)* must be able to cycle through M, any number of times. The A-arc from 91., to 91.0 Permits the necessary cycling. Another A-arc is added from 91.0 to 91., to accept the null string. These arcs are added to M, producing M 9 2 The ability to repeatedly connect machines of this form will be used in Chapter 6 to establish the equivalence of languages described by regular expressions and accepted by finite-state machines. Example 6.1.1 An NFA-, that accepts (a Ub)*ba is constructed following the steps in the recursive definition of the regular expression. The language accepted by each intermediate machine is indicated by the regular expression above the state diagram. ba (av b) (a ub)* 2 (aub)* ba 4040