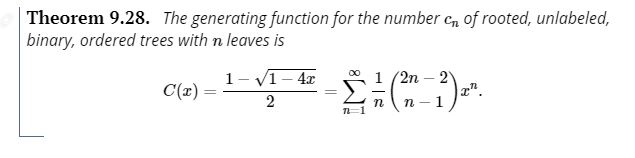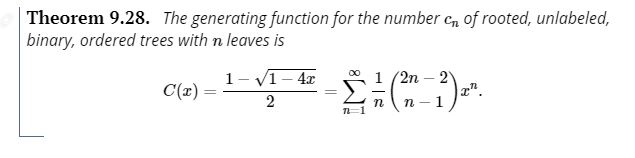
Theorem 9.28. The generating function for the number cn of rooted, unlabeled, binary, ordered trees with n leaves is C(2) 1-V1-42 2 1 /2n - 2 n n -1 5. For the purposes of this question we will defined a rooted, ordered n-ary tree as a rooted, ordered tree (same as in the textbook) where each vertex has at most n children (note that for n = 2 this definition is different than in the textbook for a binary tree, since the definition for this question allows for vertices with 1 child). For a fixed n and k > 1, let Cnek be the number of rooted, ordered, n-ary trees with exactly k vertices, and set Cn0 = 1. Let Cn(2) be the generating function for rooted, ordered, n-ary trees, ie: Cn (1) = Crete k=0 (c) When we take n = 2 we obtain a similar formula to theorem 9.28 in the textbook. Explain how what we are counting in this question is different to what is being counted in theorem 9.28. Next, explain why the formulas are similar (ie explain the relation between the definition of binary trees in this question and binary trees in the definition of this textbook, and explain how to biject between them) Theorem 9.28. The generating function for the number cn of rooted, unlabeled, binary, ordered trees with n leaves is C(2) 1-V1-42 2 1 /2n - 2 n n -1 5. For the purposes of this question we will defined a rooted, ordered n-ary tree as a rooted, ordered tree (same as in the textbook) where each vertex has at most n children (note that for n = 2 this definition is different than in the textbook for a binary tree, since the definition for this question allows for vertices with 1 child). For a fixed n and k > 1, let Cnek be the number of rooted, ordered, n-ary trees with exactly k vertices, and set Cn0 = 1. Let Cn(2) be the generating function for rooted, ordered, n-ary trees, ie: Cn (1) = Crete k=0 (c) When we take n = 2 we obtain a similar formula to theorem 9.28 in the textbook. Explain how what we are counting in this question is different to what is being counted in theorem 9.28. Next, explain why the formulas are similar (ie explain the relation between the definition of binary trees in this question and binary trees in the definition of this textbook, and explain how to biject between them)