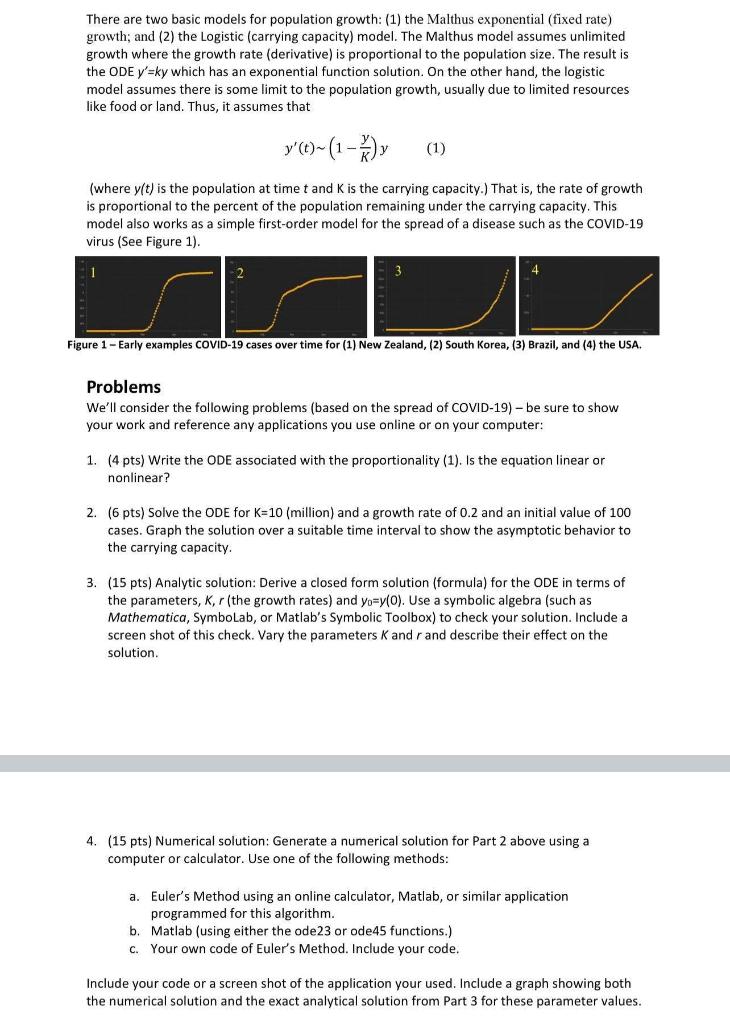
There are two basic models for population growth: (1) the Malthus exponential (fixed rate) growth; and (2) the Logistic (carrying capacity) model. The Malthus model assumes unlimited growth where the growth rate (derivative) is proportional to the population size. The result is the ODE y=ky which has an exponential function solution. On the other hand, the logistic model assumes there is some limit to the population growth, usually due to limited resources like food or land. Thus, it assumes that y(t)(1Ky)y (where y(t) is the population at time t and K is the carrying capacity.) That is, the rate of growth is proportional to the percent of the population remaining under the carrying capacity. This model also works as a simple first-order model for the spread of a disease such as the COVID-19 virus (See Figure 1). 1 Figure 1- Early examples COVID-19 cases over time for (1) New Zealand, (2) South Korea, (3) Brazil, and (4) the USA. Problems We'll consider the following problems (based on the spread of COVID-19) - be sure to show your work and reference any applications you use online or on your computer: 1. (4 pts) Write the ODE associated with the proportionality (1). Is the equation linear or nonlinear? 2. (6 pts) Solve the ODE for K=10 (million) and a growth rate of 0.2 and an initial value of 100 cases. Graph the solution over a suitable time interval to show the asymptotic behavior to the carrying capacity. 3. ( 15 pts) Analytic solution: Derive a closed form solution (formula) for the ODE in terms of the parameters, K,r (the growth rates) and y0=y(0). Use a symbolic algebra (such as Mathematica, SymboLab, or Matlab's Symbolic Toolbox) to check your solution. Include a screen shot of this check. Vary the parameters K and r and describe their effect on the solution. 4. (15 pts) Numerical solution: Generate a numerical solution for Part 2 above using a computer or calculator. Use one of the following methods: a. Euler's Method using an online calculator, Matlab, or similar application programmed for this algorithm. b. Matlab (using either the ode23 or ode45 functions.) c. Your own code of Euler's Method. Include your code. Include your code or a screen shot of the application your used. Include a graph showing both the numerical solution and the exact analytical solution from Part 3 for these parameter values. There are two basic models for population growth: (1) the Malthus exponential (fixed rate) growth; and (2) the Logistic (carrying capacity) model. The Malthus model assumes unlimited growth where the growth rate (derivative) is proportional to the population size. The result is the ODE y=ky which has an exponential function solution. On the other hand, the logistic model assumes there is some limit to the population growth, usually due to limited resources like food or land. Thus, it assumes that y(t)(1Ky)y (where y(t) is the population at time t and K is the carrying capacity.) That is, the rate of growth is proportional to the percent of the population remaining under the carrying capacity. This model also works as a simple first-order model for the spread of a disease such as the COVID-19 virus (See Figure 1). 1 Figure 1- Early examples COVID-19 cases over time for (1) New Zealand, (2) South Korea, (3) Brazil, and (4) the USA. Problems We'll consider the following problems (based on the spread of COVID-19) - be sure to show your work and reference any applications you use online or on your computer: 1. (4 pts) Write the ODE associated with the proportionality (1). Is the equation linear or nonlinear? 2. (6 pts) Solve the ODE for K=10 (million) and a growth rate of 0.2 and an initial value of 100 cases. Graph the solution over a suitable time interval to show the asymptotic behavior to the carrying capacity. 3. ( 15 pts) Analytic solution: Derive a closed form solution (formula) for the ODE in terms of the parameters, K,r (the growth rates) and y0=y(0). Use a symbolic algebra (such as Mathematica, SymboLab, or Matlab's Symbolic Toolbox) to check your solution. Include a screen shot of this check. Vary the parameters K and r and describe their effect on the solution. 4. (15 pts) Numerical solution: Generate a numerical solution for Part 2 above using a computer or calculator. Use one of the following methods: a. Euler's Method using an online calculator, Matlab, or similar application programmed for this algorithm. b. Matlab (using either the ode23 or ode45 functions.) c. Your own code of Euler's Method. Include your code. Include your code or a screen shot of the application your used. Include a graph showing both the numerical solution and the exact analytical solution from Part 3 for these parameter values







