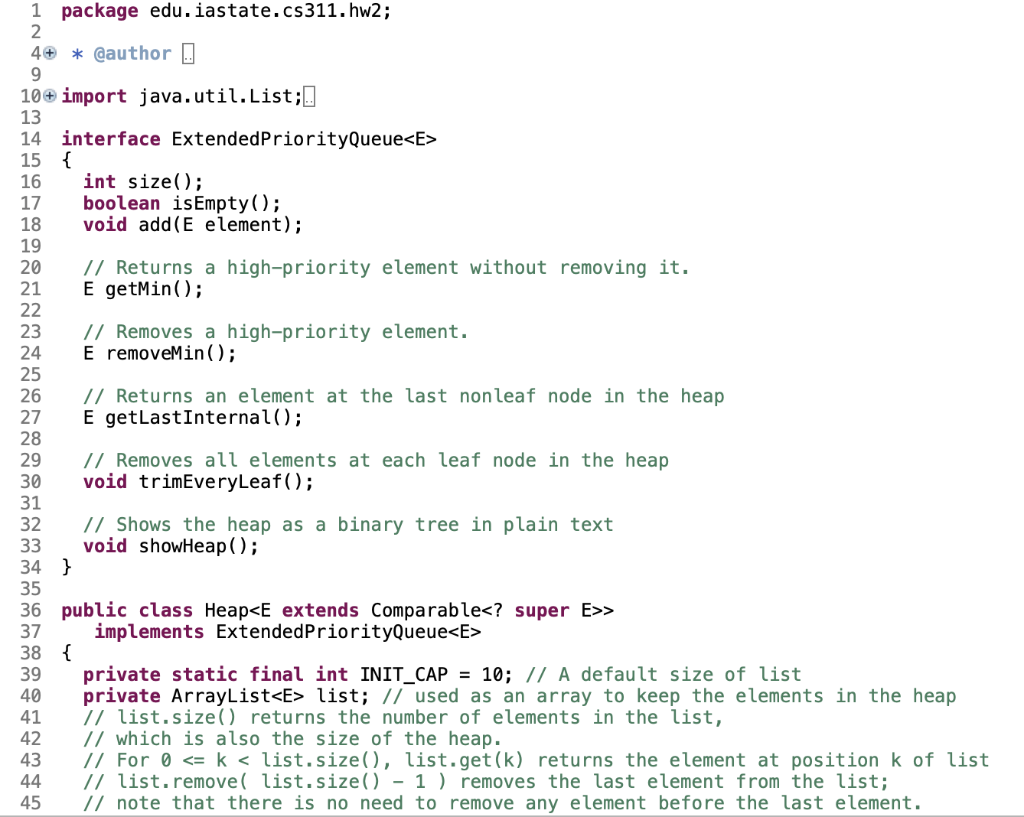
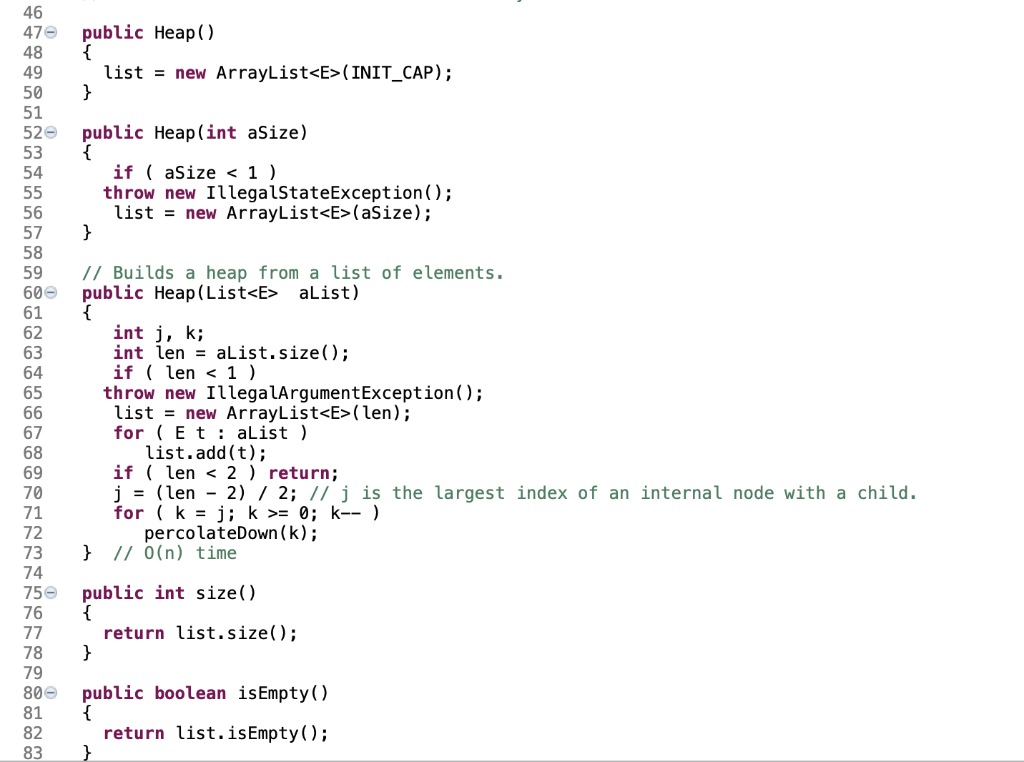
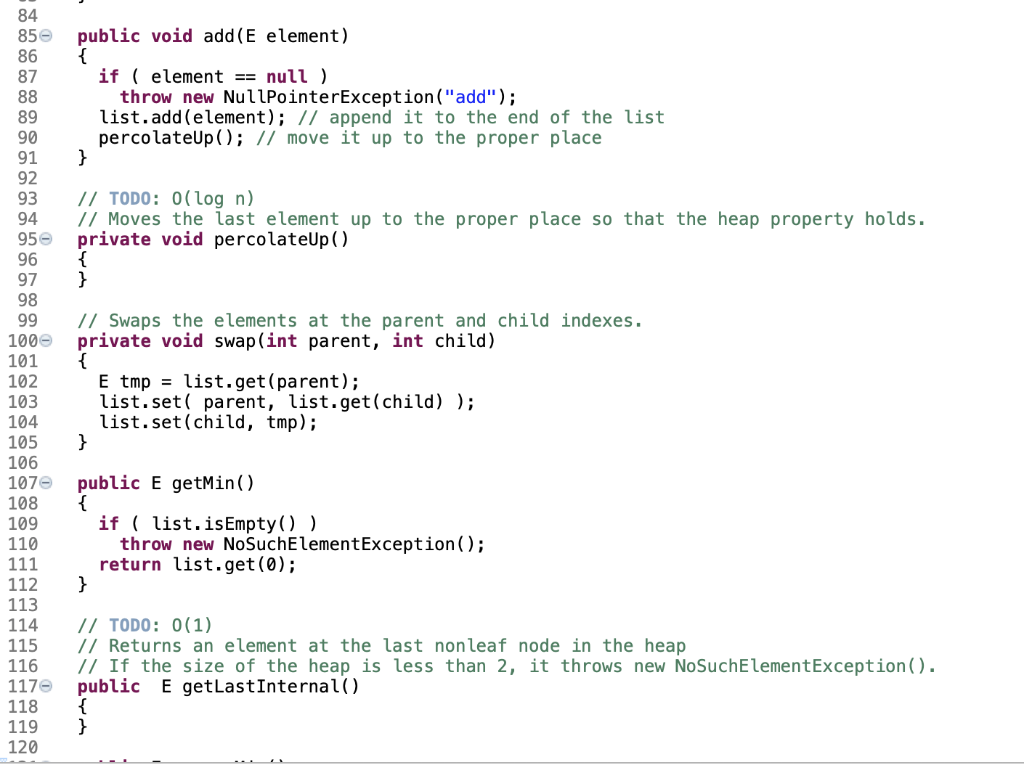
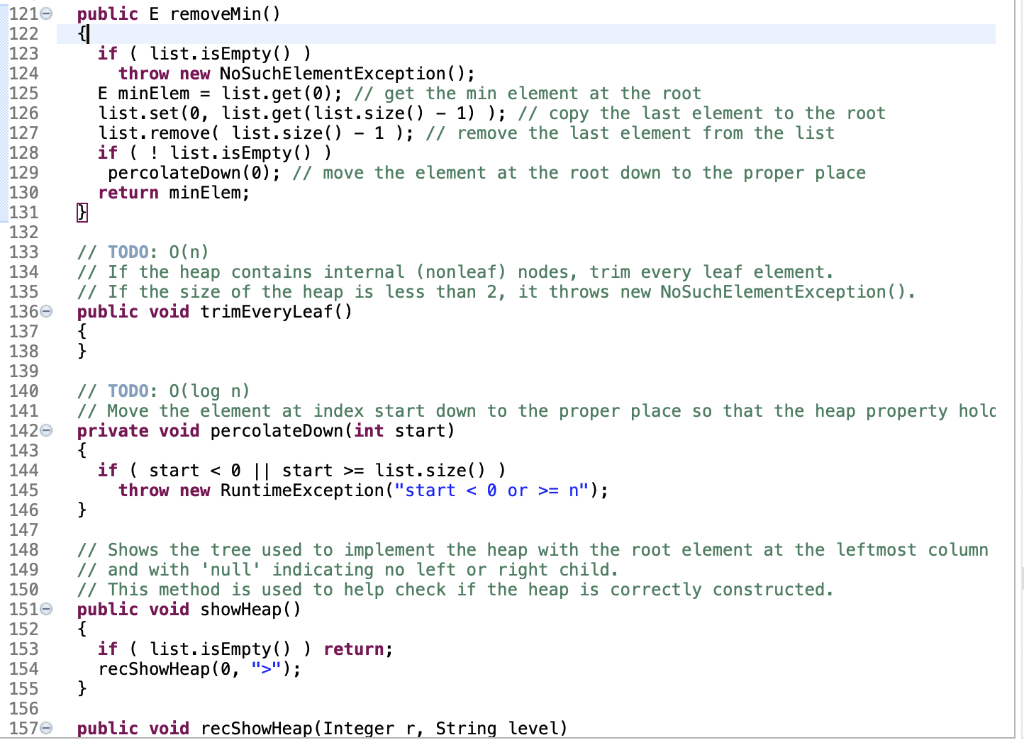
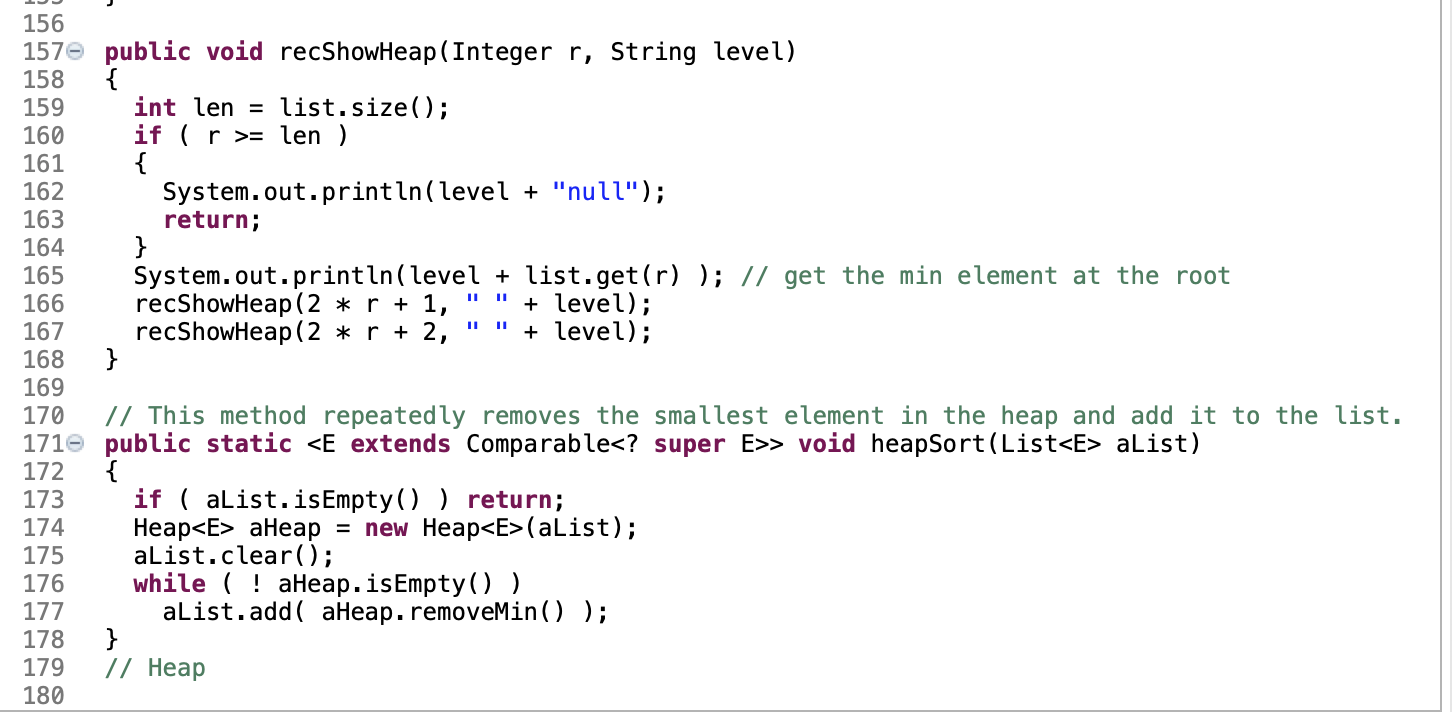
This assignment gives you an opportunity to work on the heap data structure by implementing an extended priority interface in Java. The interface is defined in a given template code segment, with many of its methods already completed. Your task is to implement the remaining methods marked by TODO before their method headings. You should study the completed methods along with comments carefully before you complete the remaining methods. Note that Java is 0-based for array and list indexes, instead of 1-based. If an array A[0..n-1) of length n is used to implement a nearly complete tree for a heap, then the index for the parent of a child at index j is [ j - 1]/2, the index for the left child of a parent at index j is 2j+1, and that for the right child is 2j+2. In the template code segment, an instance of ArrayList is used as an array list for the heap, where indexes in this array list of length n are 0,1,..., n 1. Note that if an element is removed from the heap, then an element is also removed from this array list so that the length of this array list is always the size of the heap. Below is a sample code segment to use the Heap class along with its output. 1 package edu.iastate.cs311. hw2; 2 4+ * @author . 9 10+ import java.util.List;. 13 14 interface ExtendedPriorityQueue 15 { 16 int size(); 17 boolean isEmpty(); 18 void add(E element); 19 20 // Returns a high-priority element without removing it. 21 E getMin(); 22 23 // Removes a high-priority element. 24 E removeMin(); 25 26 // Returns an element at the last non leaf node in the heap 27 E getLastInternal(); 28 29 // Removes all elements at each leaf node in the heap 30 void trimEveryLeaf(); 31 32 // Shows the heap as a binary tree in plain text 33 void showHeap(); 34 } 35 36 public class Heap> 37 implements ExtendedPriorityQueue 38 { 39 private static final int INIT_CAP = 10; // A default size of list 40 private ArrayList list; // used as an array to keep the elements in the heap 41 11 list.size() returns the number of elements in the list, 42 // which is also the size of the heap. 43 // For 0 ( INIT_CAP); } public Heap (int aSize) { if ( aSize (Size); } 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 // Builds a heap from a list of elements. public Heap (List alist) { int j, k; int len = alist.size(); if ( len (len); for ( Et alist ) list.add(t); if ( len = 0; k-- ) percolateDown (k); } // O(n) time public int size() return list.size(); } 76 77 78 79 800 81 82 83 public boolean is Empty() { return list.isEmpty(); } public void add(E element) { if ( element == null ) throw new NullPointerException("add"); list.add(element); // append it to the end of the list percolateup(); // move it up to the proper place } 84 850 86 87 88 89 90 91 92 93 94 950 96 97 98 99 1000 101 102 103 104 105 106 107 108 109 110 // TODO: 0(log n) // Moves the last element up to the proper place so that the heap property holds. private void percolateUp() { } // Swaps the elements at the parent and child indexes. private void swap(int parent, int child) { E tmp = list.get(parent); list.set( parent, list.get(child) ); list.set(child, tmp); } public E getMin() { if ( list.isEmpty()) throw new NoSuchElementException(); return list.get(0); } 111 112 113 114 115 116 117 118 119 120 // TODO: 0(1) // Returns an element at the last non leaf node in the heap // If the size of the heap is less than 2, it throws new NoSuchElementException(). public E getLastInternal() { } public E removeMin() { if ( list.isEmpty()) throw new No SuchElementException(); E minElem = list.get(0); // get the min element at the root list.set(0, list.get(list.size() - 1) ); // copy the last element to the root list.remove( list.size() - 1); // remove the last element from the list if ( ! list.isEmpty() ) percolateDown(0); // move the element at the root down to the proper place return minElem; // TODO: O(n) // If the heap contains internal (non leaf) nodes, trim every leaf element. // If the size of the heap is less than 2, it throws new No SuchElementException(). public void trimEveryLeaf () { } 1210 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 1510 152 153 154 155 156 157 // TODO: O(log n) // Move the element at index start down to the proper place so that the heap property holo private void percolateDown (int start) { if ( start = list.size() ) throw new RuntimeException("start = n"); } // Shows the tree used to implement the heap with the root element at the leftmost column // and with 'null' indicating no left or right child. // This method is used to help check if the heap is correctly constructed. public void showHeap() { if ( list.isEmpty()) return; recShowHeap(,""); } public void recShowHeap (Integer r, String level) 156 157e public void recShowHeap (Integer r, String level) 158 { 159 int len = list.size(); 160 if ( r >= len ) 161 { 162 System.out.println(level + "null"); 163 return; 164 } 165 System.out.println(level + list.get(r) ); // get the min element at the root 166 recShowHeap(2 * r + 1, + level); 167 recShowHeap(2 * r + 2, + level); 168 } 169 170 // This method repeatedly removes the smallest element in the heap and add it to the list. 171e public static > void heapSort(List alist) 172 { 173 if ( alist.isEmpty ( ) return; 174 Heap aheap = new Heap(alist); 175 alist.clear(); 176 while (! aheap.isEmpty() ) 177 aList.add( aHeap.removeMin() ); 178 } 179 // Heap 180 This assignment gives you an opportunity to work on the heap data structure by implementing an extended priority interface in Java. The interface is defined in a given template code segment, with many of its methods already completed. Your task is to implement the remaining methods marked by TODO before their method headings. You should study the completed methods along with comments carefully before you complete the remaining methods. Note that Java is 0-based for array and list indexes, instead of 1-based. If an array A[0..n-1) of length n is used to implement a nearly complete tree for a heap, then the index for the parent of a child at index j is [ j - 1]/2, the index for the left child of a parent at index j is 2j+1, and that for the right child is 2j+2. In the template code segment, an instance of ArrayList is used as an array list for the heap, where indexes in this array list of length n are 0,1,..., n 1. Note that if an element is removed from the heap, then an element is also removed from this array list so that the length of this array list is always the size of the heap. Below is a sample code segment to use the Heap class along with its output. 1 package edu.iastate.cs311. hw2; 2 4+ * @author . 9 10+ import java.util.List;. 13 14 interface ExtendedPriorityQueue 15 { 16 int size(); 17 boolean isEmpty(); 18 void add(E element); 19 20 // Returns a high-priority element without removing it. 21 E getMin(); 22 23 // Removes a high-priority element. 24 E removeMin(); 25 26 // Returns an element at the last non leaf node in the heap 27 E getLastInternal(); 28 29 // Removes all elements at each leaf node in the heap 30 void trimEveryLeaf(); 31 32 // Shows the heap as a binary tree in plain text 33 void showHeap(); 34 } 35 36 public class Heap> 37 implements ExtendedPriorityQueue 38 { 39 private static final int INIT_CAP = 10; // A default size of list 40 private ArrayList list; // used as an array to keep the elements in the heap 41 11 list.size() returns the number of elements in the list, 42 // which is also the size of the heap. 43 // For 0 ( INIT_CAP); } public Heap (int aSize) { if ( aSize (Size); } 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 // Builds a heap from a list of elements. public Heap (List alist) { int j, k; int len = alist.size(); if ( len (len); for ( Et alist ) list.add(t); if ( len = 0; k-- ) percolateDown (k); } // O(n) time public int size() return list.size(); } 76 77 78 79 800 81 82 83 public boolean is Empty() { return list.isEmpty(); } public void add(E element) { if ( element == null ) throw new NullPointerException("add"); list.add(element); // append it to the end of the list percolateup(); // move it up to the proper place } 84 850 86 87 88 89 90 91 92 93 94 950 96 97 98 99 1000 101 102 103 104 105 106 107 108 109 110 // TODO: 0(log n) // Moves the last element up to the proper place so that the heap property holds. private void percolateUp() { } // Swaps the elements at the parent and child indexes. private void swap(int parent, int child) { E tmp = list.get(parent); list.set( parent, list.get(child) ); list.set(child, tmp); } public E getMin() { if ( list.isEmpty()) throw new NoSuchElementException(); return list.get(0); } 111 112 113 114 115 116 117 118 119 120 // TODO: 0(1) // Returns an element at the last non leaf node in the heap // If the size of the heap is less than 2, it throws new NoSuchElementException(). public E getLastInternal() { } public E removeMin() { if ( list.isEmpty()) throw new No SuchElementException(); E minElem = list.get(0); // get the min element at the root list.set(0, list.get(list.size() - 1) ); // copy the last element to the root list.remove( list.size() - 1); // remove the last element from the list if ( ! list.isEmpty() ) percolateDown(0); // move the element at the root down to the proper place return minElem; // TODO: O(n) // If the heap contains internal (non leaf) nodes, trim every leaf element. // If the size of the heap is less than 2, it throws new No SuchElementException(). public void trimEveryLeaf () { } 1210 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 1510 152 153 154 155 156 157 // TODO: O(log n) // Move the element at index start down to the proper place so that the heap property holo private void percolateDown (int start) { if ( start = list.size() ) throw new RuntimeException("start = n"); } // Shows the tree used to implement the heap with the root element at the leftmost column // and with 'null' indicating no left or right child. // This method is used to help check if the heap is correctly constructed. public void showHeap() { if ( list.isEmpty()) return; recShowHeap(,""); } public void recShowHeap (Integer r, String level) 156 157e public void recShowHeap (Integer r, String level) 158 { 159 int len = list.size(); 160 if ( r >= len ) 161 { 162 System.out.println(level + "null"); 163 return; 164 } 165 System.out.println(level + list.get(r) ); // get the min element at the root 166 recShowHeap(2 * r + 1, + level); 167 recShowHeap(2 * r + 2, + level); 168 } 169 170 // This method repeatedly removes the smallest element in the heap and add it to the list. 171e public static > void heapSort(List alist) 172 { 173 if ( alist.isEmpty ( ) return; 174 Heap aheap = new Heap(alist); 175 alist.clear(); 176 while (! aheap.isEmpty() ) 177 aList.add( aHeap.removeMin() ); 178 } 179 // Heap 180