This assignment will consist of two parts. In the first, we will develop an algorithm to check whether a given binary tree has the BST property (we have carelessly relied on this in the lectures, it is time to check!). In the second part, we will see how some important operations that can be performed with sorted arrays efficiently can also be performed with BST's efficiently.

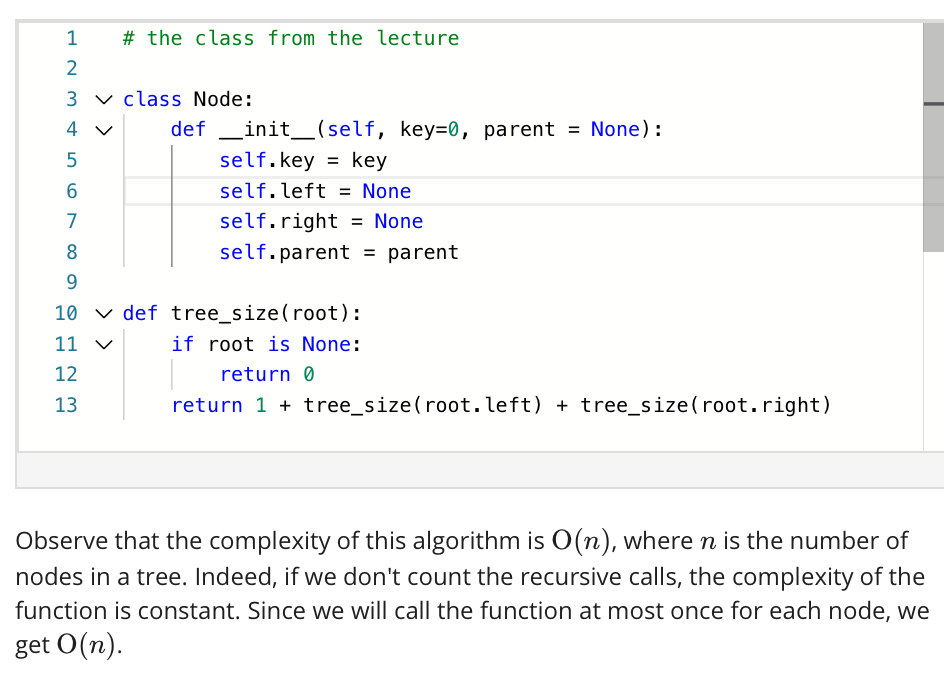
We will aim at making the algorithms linear in the number of nodes in the tree. The algorithm below that computes the size of a binary tree is a template for all the problems in this assignment.

.

#Part 1. Write a function count_distinct(T) that takes as input a binary search tree T and computes the number of distinct keys present in the tree.

Hint: again, start with a similar auxiliary function and the use the same strategy as tree_size.

#Part 2. Write a function check_BST(T) (T is a binary tree as in Part 1) that returns True if T is a BST and False otherwise.

Caveats:

• It is not enough to check that the key at each node is at most the key of the right child and at least the key of the left child. It has to be at most any key in the right subtree and at least any key in the left subtree.
• You might want to use the function tree_max from the Part 1 but this will likely damage your complexity

#Part 3. Write a function min_diff(T) that takes as input a binary search tree T and computes the smallest absolute value of the difference between the keys in different nodes.

Hint: start with an auxiliary function similarly to Part 2.

Hint: start with writing an auxiliary function _check_BST that will return a triple: whether the tree is BST or not, the minimum, and the maximum in the tree. Computing this function can be arranged in a similar fashion to tree_size.

#Part 4. Write a function tree_max(T), where T is an instance of the Node class representing a binary tree (not necessarily a BST!), that find the largest number in the tree. For empty tree, we set the max to be -math.inf.

Sample/Example:

import math

class Node:

def __init__(self, key=0, parent = None):

self.key = key

self.left = None

self.right = None

self.parent = parent

def insert(root, node):

if root.key > node.key:

if root.left == None:

root.left = node

node.parent = root

else:

insert(root.left, node)

else:

if root.right == None:

root.right = node

node.parent = root

else:

insert(root.right, node)

#######################################################

def tree_size(root):

pass

def tree_max(root):

pass

def _check_BST(root):

pass

def check_BST(root):

return _check_BST(root)[0]

def _min_diff(root):

pass

def min_diff(root):

return _min_diff(root)[0]

#################################################

if __name__ == "__main__":

T = Node(3)

insert(T, Node(1))

insert(T, Node(2))

# should print True

print(check_BST(T))

# should print 1

print(min_diff(T))

1 # the class from the lecture 2 3 v class Node: 4 v def __init__(self, key=0, parent = None): 5 self.key = key 6 self. left = None 7 self.right = None 8 self.parent = parent 9 10 v def tree_size(root): 11 v if root is None: 12 return 0 13 return 1 + tree_size(root. left) + tree_size(root.right) Observe that the complexity of this algorithm is O(n), where n is the number of nodes in a tree. Indeed, if we don't count the recursive calls, the complexity of the function is constant. Since we will call the function at most once for each node, we get O(n)