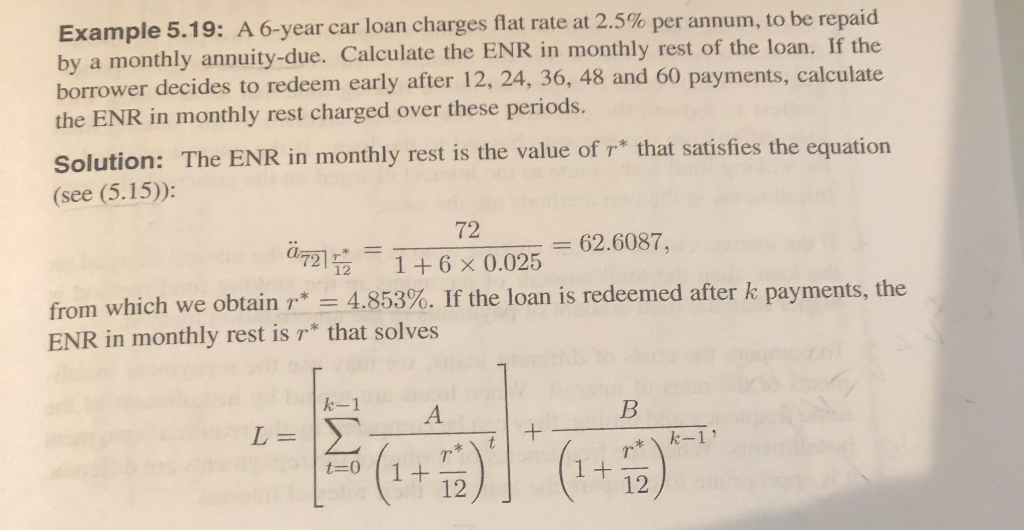this example involves the Rule of 78. if you solve this by creating an excel document that would be helpful. I am having trouble calculating r*.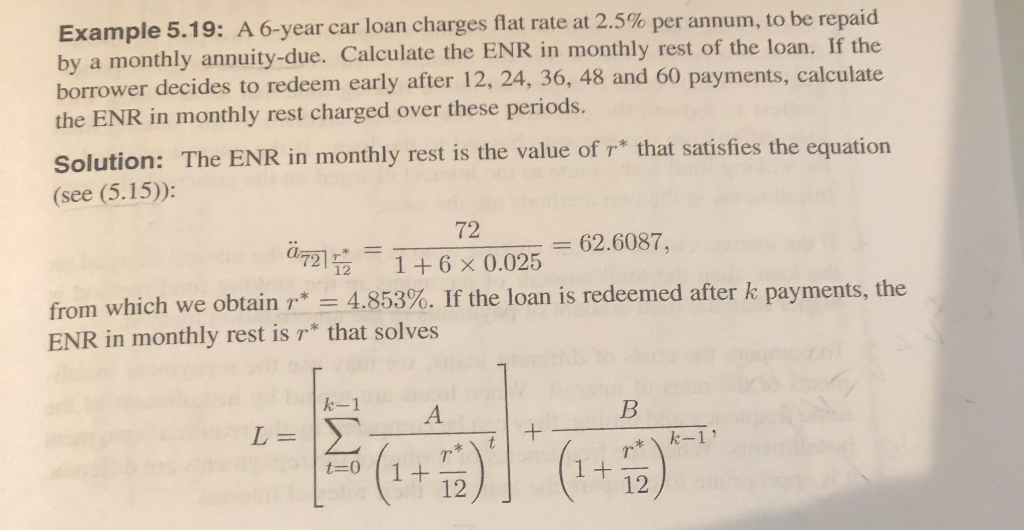

Example 5.19: A 6-year car loan charges flat rate at 2.5% per annum, to be repaid by a monthly annuity-due. Calculate the ENR in monthly rest of the loan. If the borrower decides to redeem early after 12, 24, 36, 48 and 60 payments, calculate the ENR in monthly rest charged over these periods. Solution: The ENR in monthly rest is the value of r* that satisfies the equation (see (5.15)): 72 F = 62.6087, 0721= 1+ 6 x 0.025 from which we obtain r* = 4.853%. If the loan is redeemed after k payments, the ENR in monthly rest is r* that solves L = +- p* \ k-1 1 + where A and B are given in (5.13) and (5.17), respectively, Solving the abe equation for various values of k we obtain the following results: 1 12 5.369 24 5,085 36 4.972 48 4.906 60 4.867 p* (%) 12 If the loan is redeemed at maturity, the annual effective rate of interest is (1 * 0.04853 ) 12 - 1 = 4.9624%. However, if the loan is redeemed after 1 year, the effective rate of interest is (1 + 0.00369)12 - 1 = 5.5503%. In the case the loan involves a further penalty for early redemption, the difference in the borrowing costs may be even higher. Example 5.19: A 6-year car loan charges flat rate at 2.5% per annum, to be repaid by a monthly annuity-due. Calculate the ENR in monthly rest of the loan. If the borrower decides to redeem early after 12, 24, 36, 48 and 60 payments, calculate the ENR in monthly rest charged over these periods. Solution: The ENR in monthly rest is the value of r* that satisfies the equation (see (5.15)): 72 F = 62.6087, 0721= 1+ 6 x 0.025 from which we obtain r* = 4.853%. If the loan is redeemed after k payments, the ENR in monthly rest is r* that solves L = +- p* \ k-1 1 + where A and B are given in (5.13) and (5.17), respectively, Solving the abe equation for various values of k we obtain the following results: 1 12 5.369 24 5,085 36 4.972 48 4.906 60 4.867 p* (%) 12 If the loan is redeemed at maturity, the annual effective rate of interest is (1 * 0.04853 ) 12 - 1 = 4.9624%. However, if the loan is redeemed after 1 year, the effective rate of interest is (1 + 0.00369)12 - 1 = 5.5503%. In the case the loan involves a further penalty for early redemption, the difference in the borrowing costs may be even higher