Question: This is a strictly individual assignment. That means, you are not allowed to take a peek at any solutions, including online resources, and you are



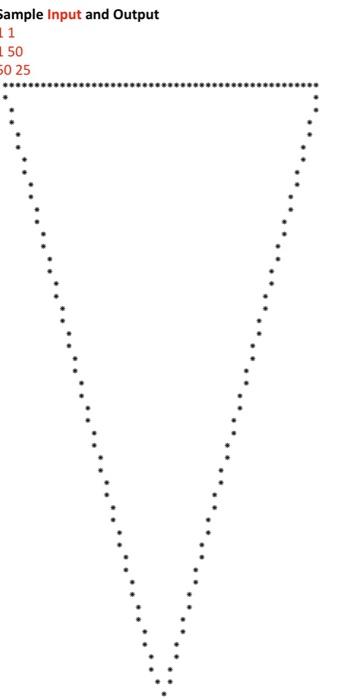

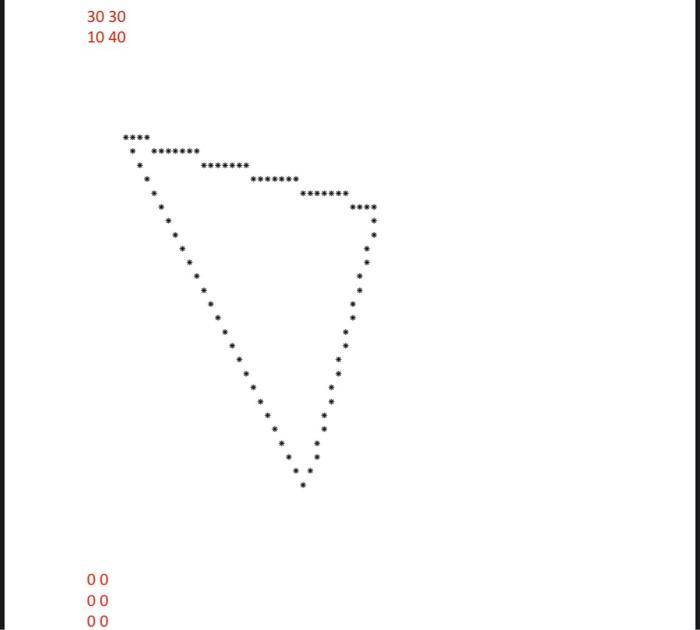


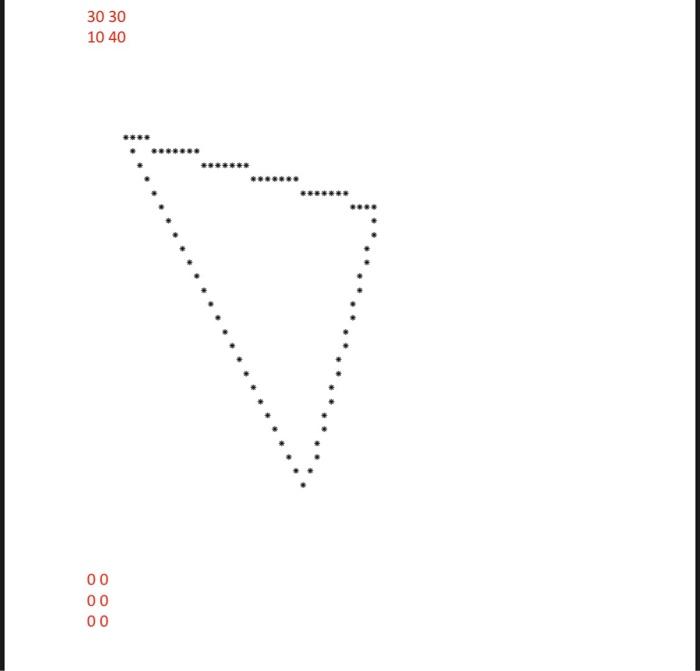
This is a strictly individual assignment. That means, you are not allowed to take a peek at any solutions, including online resources, and you are not allowed to share your answers with anyone, including your classmates. You are not allowed to program together with your friends or relatives. You are only allowed to use your lecture notes and the textbook. Failure to follow these rules will result in getting only 1 point for the project. Problem Description: We would like to write a graphics program which draws a user entered triangle on a 51x51 grid. The program should be modular and use methods for subtasks. The program has three main layers: 1. User interface which asks the user to enter individual points that constitute the three nodes of a triangle. 2. Rendering the geometric triangle with three lines on the 51x51 display matrix 3. Displaying the matrix on the user's console as a text output using characters. 1. User Interface (main method): This should repetitively accept from the user 6 numbers that are the coordinate of the three nodes of a triangle until all 6 numbers are zero in which case the program should terminate. In every other case the program creates and draws the triangle given by the coordinates of its three nodes and proceeds to get the next 6 numbers. 2. Rendering: The triangles are created in a 51x51 boolean matrix that holds the image of the drawing. 1. Write a method clearMatrix(matrix) that clears (i.e., sets to false) all the entries of the matrix. This method should be invoked at the beginning of every drawing so that to clear the image that possibly contains the previously drawn triangle. 2. Write a method drawLine(matrix, x0, y0, x1, y1) which takes in a 2D Matrix, and the coordinates of two points and draws the line between them by marking (i.e., setting to true) every point in the line. 3. Output: Write a method printMatrix(matrix) that prints the content of the matrix to the user's console. The rest of the document discusses the drawline method. The following is the pseudo-code (not Java code) of a nave algorithm to draw a line between two given points. Pseudocode Algorithm for Line Drawing drawline{matrix, XO, yo, x1, y1) dx = x2-x1 dy - y2-yi for x from x1 to x2 y v1 + dy * (x - 1)/dx mark(matrix, xy) For example drawLine(mat,1,2,5,6) method generates the following matrix where F denotes a "false" entry and T denotes a "true" entry (the entire 51x51 matrix is not shown here). FFFFFFFFFFFFF ... FFTFFFFFFFF FFFTFFFFFFF FFFFTFFFFFF FFFFFTFFFFF FFFFFF F F F F FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF F F The above nave algorithm works well if there is one marked point at each vertical line as it is the case in the previous example. Note that the code marks exactly one point at each iteration which in turn corresponds to a vertical line. However, sometimes more than one point should be marked on a vertical line. The most prominent example is the example of a vertical line, for example between the points (1,1) (1,5). It is clear that this code is not usable in this exemple. FFFFFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF F F A similar situation arises when the line is not vertical but still steep, for example between the points (1,1) (2,5). FFFFFFFFFFFFF ... FTFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FFTFFFFFFFF FFTFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF F F In such cases there is a simple solution: just exchange the roles for the x and y coordinates. The general rule is that if the slope of the line is between-1 and 1 we can use the normal algorithm. Otherwise the line is steep in which case we can still use the same algorithm after exchanging the roles of the x and y coordinates. Namely, we will mark one point for each horizontal line. Recall that the slope of a line between two points (X,Y,) and (x,y) is Note that this corresponds to the ratio dy/dx in terms of the variables in the pseudo-code. Note also that the denominator might be zero in which case you cannot use the division operator slope=-1 slope=1 STEEP NORMAL NORMAL X STEEP Sample input and Output 11 150 50 25 1 50 50 50 55 30 30 10 40 *** ******* 00 00 00 dx = x2-x1 dy-y2-yi for x from x1 to x2 yeyidy * (x - xl) / dx mark(matrix, xy) For example drawLine(mat,1,2,5,6) method generates the following matrix where F denotes a "false" entry and T denotes a "true" entry (the entire 51x51 matrix is not shown here). FFFFFFFFFFFFF ... FFTFFFFFFFF FFFFFFFFFF F F F F T F F F F F F FFFFFTFFFFF FFFFFF F F F F FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF F F The above nave algorithm works well if there is one marked point at each vertical line as it is the case in the previous example. Note that the code marks exactly one point at each iteration which in turn corresponds to a vertical line. However, sometimes more than one point should be marked on a vertical line. The most prominent example is the example of a vertical line, for example between the points (1,1) (1,5). It is clear that this code is not usable in this exemple. FFFFFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF F F A similar situation arises when the line is not vertical but still steep, for example between the points (1.1) (2,5). FFFFFFFFFFFFF ... FTFFFFFFFFF FTFFFFFFFFF FTFFFFFFFFF FFTFFFFFFFF FFTFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF FFFFFFFFFFF F F In such cases there is a simple solution: just exchange the roles for the x and y coordinates. The general rule is that if the slope of the line is between-1 and 1 we can use the normal algorithm. Otherwise the line is steep in which case we can still use the same algorithm after exchanging the roles of the x and y coordinates. Namely, we will mark one point for each horizontal line. Recall that the slope of a line between two points (xXx) and (x2Yz) is Note that this corresponds to the ratio dy/dx in terms of the variables in the pseudo-code. Note also that the denominator might be zero in which case you cannot use the division operator. slope=-1 slope=1 STEEP NORMAL NORMAL STEEP 30 30 10 40 *** 00 00 00
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


