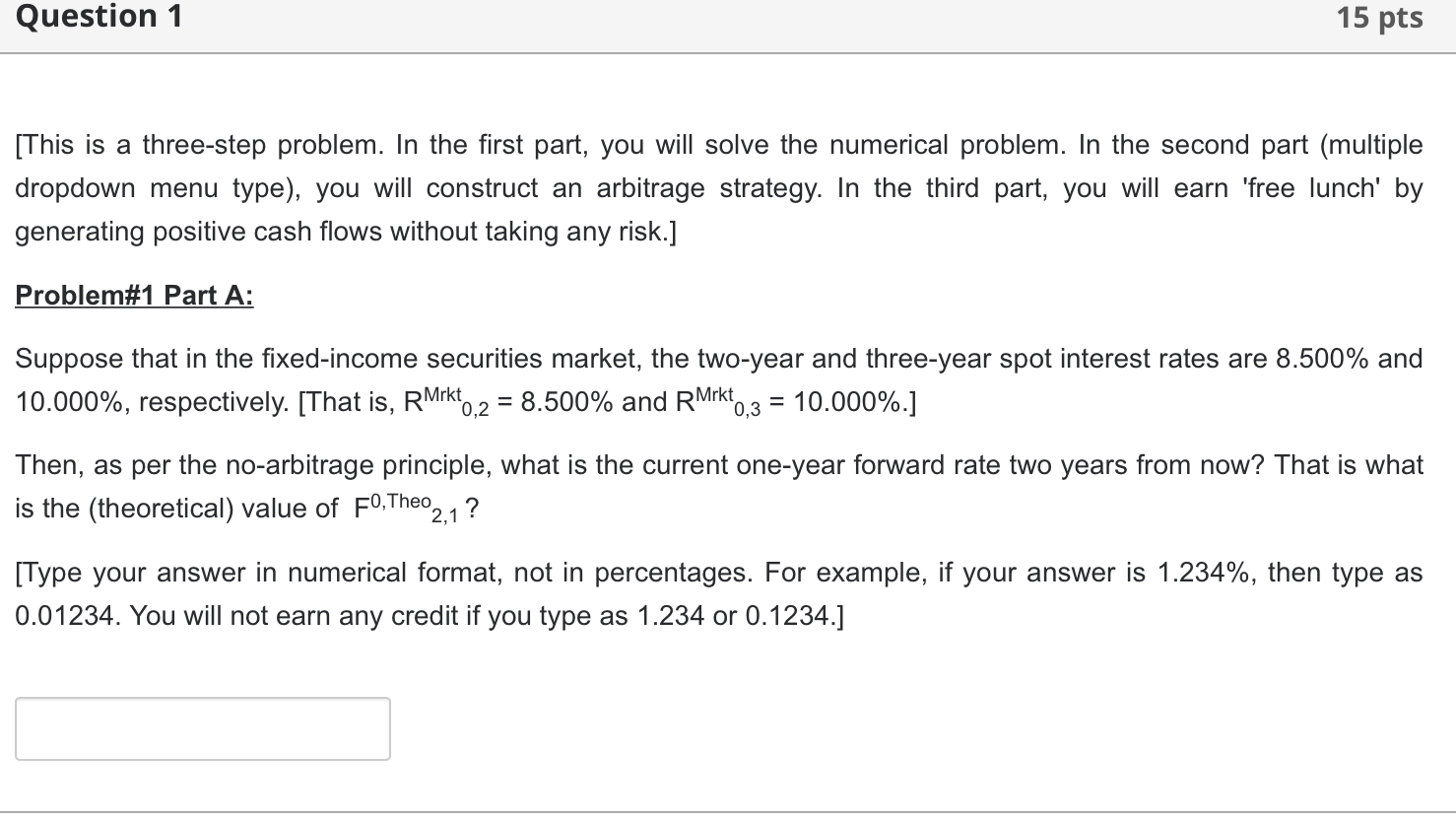
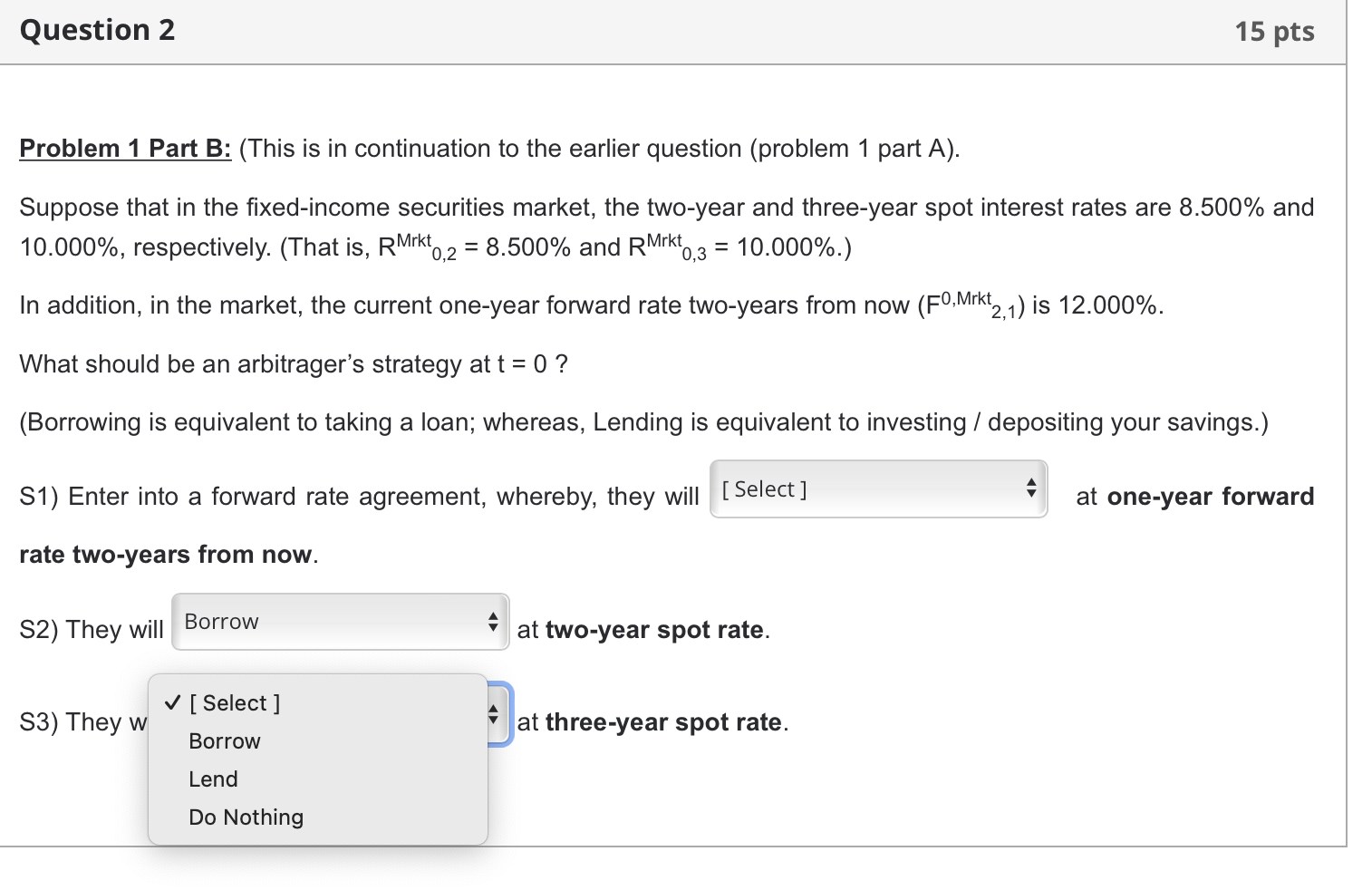
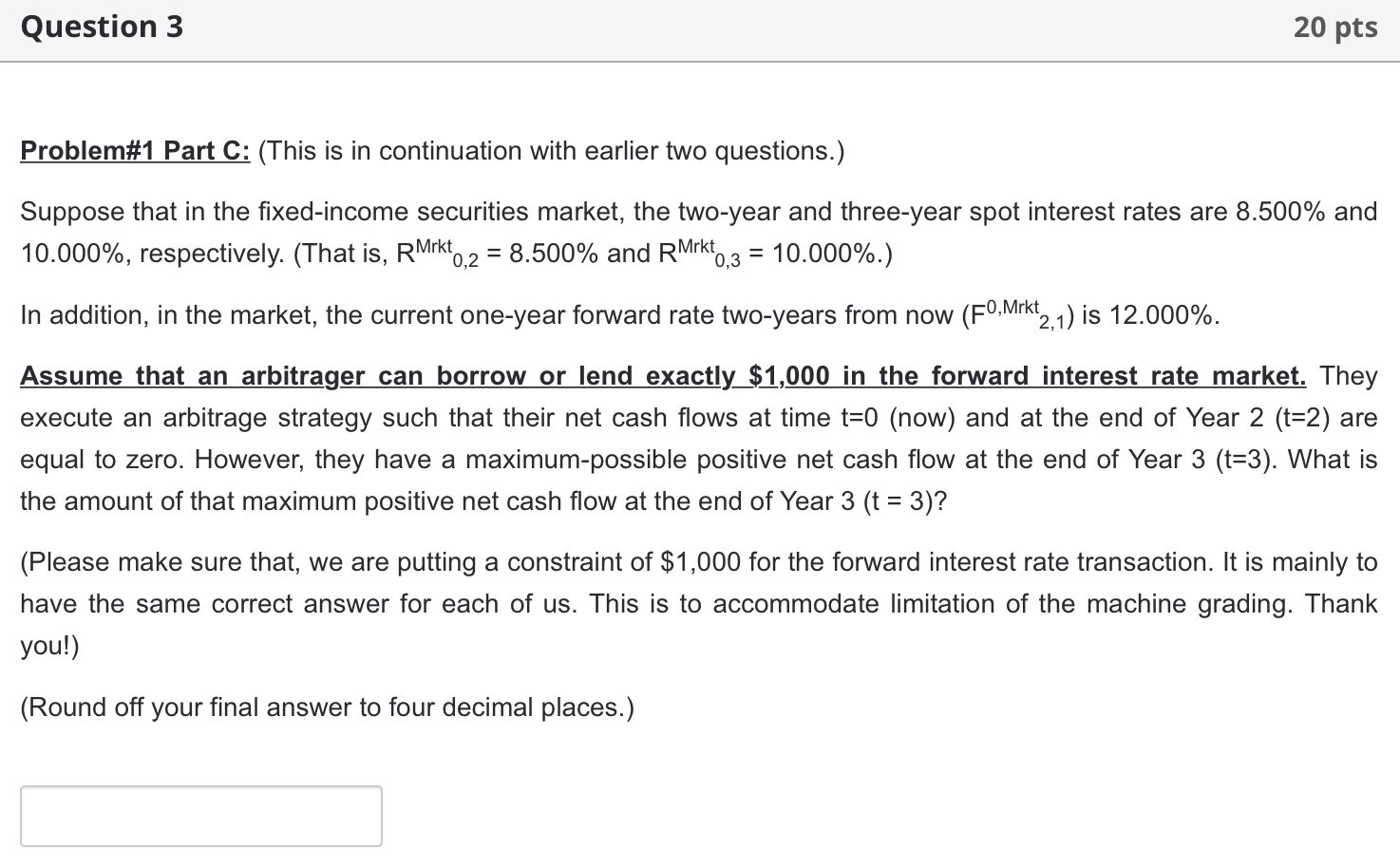
[This is a three-step problem. In the first part, you will solve the numerical problem. In the second part (multiple dropdown menu type), you will construct an arbitrage strategy. In the third part, you will earn 'free lunch' by generating positive cash flows without taking any risk.] Problem\#1 Part A: Suppose that in the fixed-income securities market, the two-year and three-year spot interest rates are 8.500% and 10.000%, respectively. [That is, RMrkt0,2=8.500% and RMrkt0,3=10.000%.] Then, as per the no-arbitrage principle, what is the current one-year forward rate two years from now? That is what is the (theoretical) value of F0,Theo 2,1 ? [Type your answer in numerical format, not in percentages. For example, if your answer is 1.234%, then type as 0.01234. You will not earn any credit if you type as 1.234 or 0.1234.] Problem 1 Part B: (This is in continuation to the earlier question (problem 1 part A). Suppose that in the fixed-income securities market, the two-year and three-year spot interest rates are 8.500% and 10.000%, respectively. (That is, RMrkt0,2=8.500% and R0,3Mrkt0,3=10.000%.) In addition, in the market, the current one-year forward rate two-years from now (F0,Mrkt2,1) is 12.000%. What should be an arbitrager's strategy at t=0 ? (Borrowing is equivalent to taking a loan; whereas, Lending is equivalent to investing / depositing your savings.) S1) Enter into a forward rate agreement, whereby, they will at one-year forward rate two-years from now. S2) They will at two-year spot rate. S3) They w at three-year spot rate. Problem\#1 Part C: (This is in continuation with earlier two questions.) Suppose that in the fixed-income securities market, the two-year and three-year spot interest rates are 8.500% and 10.000%, respectively. (That is, RMrkt0,2=8.500% and RMrkt0,3=10.000%.) In addition, in the market, the current one-year forward rate two-years from now (F0,Mrkt2,1) is 12.000%. Assume that an arbitrager can borrow or lend exactly $1,000 in the forward interest rate market. They execute an arbitrage strategy such that their net cash flows at time t=0 (now) and at the end of Year 2 ( t=2) are equal to zero. However, they have a maximum-possible positive net cash flow at the end of Y ( 3 ( =3). What is the amount of that maximum positive net cash flow at the end of Year 3(t=3) ? (Please make sure that, we are putting a constraint of $1,000 for the forward interest rate transaction. It is mainly to have the same correct answer for each of us. This is to accommodate limitation of the machine grading. Thank you!) (Round off your final answer to four decimal places.) [This is a three-step problem. In the first part, you will solve the numerical problem. In the second part (multiple dropdown menu type), you will construct an arbitrage strategy. In the third part, you will earn 'free lunch' by generating positive cash flows without taking any risk.] Problem\#1 Part A: Suppose that in the fixed-income securities market, the two-year and three-year spot interest rates are 8.500% and 10.000%, respectively. [That is, RMrkt0,2=8.500% and RMrkt0,3=10.000%.] Then, as per the no-arbitrage principle, what is the current one-year forward rate two years from now? That is what is the (theoretical) value of F0,Theo 2,1 ? [Type your answer in numerical format, not in percentages. For example, if your answer is 1.234%, then type as 0.01234. You will not earn any credit if you type as 1.234 or 0.1234.] Problem 1 Part B: (This is in continuation to the earlier question (problem 1 part A). Suppose that in the fixed-income securities market, the two-year and three-year spot interest rates are 8.500% and 10.000%, respectively. (That is, RMrkt0,2=8.500% and R0,3Mrkt0,3=10.000%.) In addition, in the market, the current one-year forward rate two-years from now (F0,Mrkt2,1) is 12.000%. What should be an arbitrager's strategy at t=0 ? (Borrowing is equivalent to taking a loan; whereas, Lending is equivalent to investing / depositing your savings.) S1) Enter into a forward rate agreement, whereby, they will at one-year forward rate two-years from now. S2) They will at two-year spot rate. S3) They w at three-year spot rate. Problem\#1 Part C: (This is in continuation with earlier two questions.) Suppose that in the fixed-income securities market, the two-year and three-year spot interest rates are 8.500% and 10.000%, respectively. (That is, RMrkt0,2=8.500% and RMrkt0,3=10.000%.) In addition, in the market, the current one-year forward rate two-years from now (F0,Mrkt2,1) is 12.000%. Assume that an arbitrager can borrow or lend exactly $1,000 in the forward interest rate market. They execute an arbitrage strategy such that their net cash flows at time t=0 (now) and at the end of Year 2 ( t=2) are equal to zero. However, they have a maximum-possible positive net cash flow at the end of Y ( 3 ( =3). What is the amount of that maximum positive net cash flow at the end of Year 3(t=3) ? (Please make sure that, we are putting a constraint of $1,000 for the forward interest rate transaction. It is mainly to have the same correct answer for each of us. This is to accommodate limitation of the machine grading. Thank you!) (Round off your final answer to four decimal places.)