this is heat transfer book problem,need thr euqations for those problems to for a metrix, no more information is needed

Write a MATLAB CODE for either Problem 4.45 or 4.48 from the sixth edition of the textbook . Solve the problems by using two different sets of values for Dx and Dy (i.e., perform a grid resolution analysis)

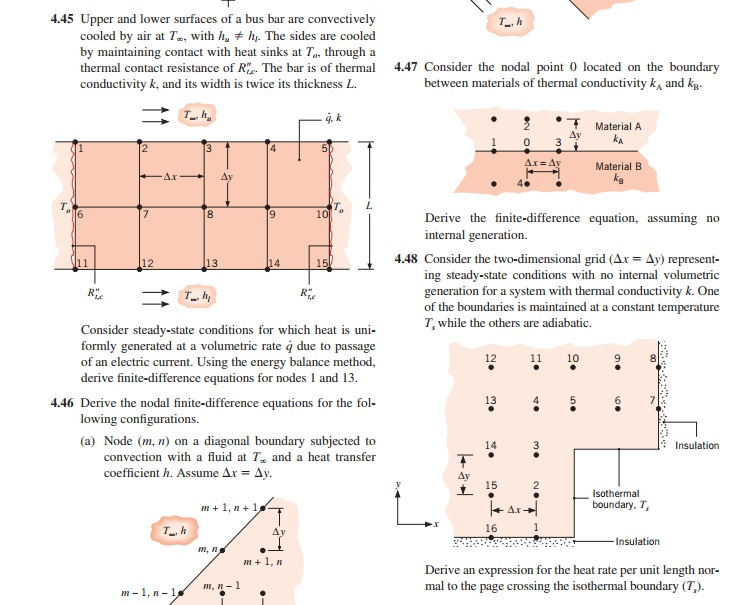
4.45 Upper and lower surfaces of a bus bar are convectively cooled by air at T, with h + h. The sides are cooled by maintaining contact with heat sinks at To, through a thermal contact resistance of R. The bar is of therma 4.47 Consider the nodal point 0 located on the boundary conductivity k, and its width is twice its thickness L. between materials of thermal conductivity k and kB T Material A Ay 0 Material B Derive the finite-difference equation, assuming no internal generation. 4.48 Consider the two-dimensional grid (Ar-Ay) represent- ing steady-state conditions with no internal volumetric generation for a system with thermal conductivity k. One of the boundaries is maintained at a constant temperature T, while the others are adiabatic. Consider steady-state conditions for which heat is uni- formly generated at a volumetric rate q due to passage of an electric current. Using the energy balance method, derive finite-difference equations for nodes 1 and 13 12 10 13 6 4.46 Derive the nodal finite-difference equations for the fol- lowing configurations. (a) Node (m, n) on a diagonal boundary subjected to 14 Insulation convection with a fluid at T and a heat transfer coefficient h. Assume ArAy. 15 m1,n 1 boundary, T, 16 Insulation m1, n Derive an expression for the heat rate per unit length nor- mal to the page crossing the isothermal boundary (T). 4.45 Upper and lower surfaces of a bus bar are convectively cooled by air at T, with h + h. The sides are cooled by maintaining contact with heat sinks at To, through a thermal contact resistance of R. The bar is of therma 4.47 Consider the nodal point 0 located on the boundary conductivity k, and its width is twice its thickness L. between materials of thermal conductivity k and kB T Material A Ay 0 Material B Derive the finite-difference equation, assuming no internal generation. 4.48 Consider the two-dimensional grid (Ar-Ay) represent- ing steady-state conditions with no internal volumetric generation for a system with thermal conductivity k. One of the boundaries is maintained at a constant temperature T, while the others are adiabatic. Consider steady-state conditions for which heat is uni- formly generated at a volumetric rate q due to passage of an electric current. Using the energy balance method, derive finite-difference equations for nodes 1 and 13 12 10 13 6 4.46 Derive the nodal finite-difference equations for the fol- lowing configurations. (a) Node (m, n) on a diagonal boundary subjected to 14 Insulation convection with a fluid at T and a heat transfer coefficient h. Assume ArAy. 15 m1,n 1 boundary, T, 16 Insulation m1, n Derive an expression for the heat rate per unit length nor- mal to the page crossing the isothermal boundary (T)