This is only one question, I explained the question in the detailed formated with instructions and example, you only have to edit the given code to get the similar output in the example. Please help answer it in step by step format. Thank you!!

Finding the minimum spanning tree of a undirected weighted graph. A weighted graph is a graph that has a numerical weight property on each edge. The minimum spanning tree (MST) of an undirected weighted graph is a tree that connects all nodes in the graph, and at the same time minimizing the sum of the weights of the tree's edges. Many important problems in computer networking and operations research boil down to finding MSTs on graphs. As an example, this is a undirected weighted graph:

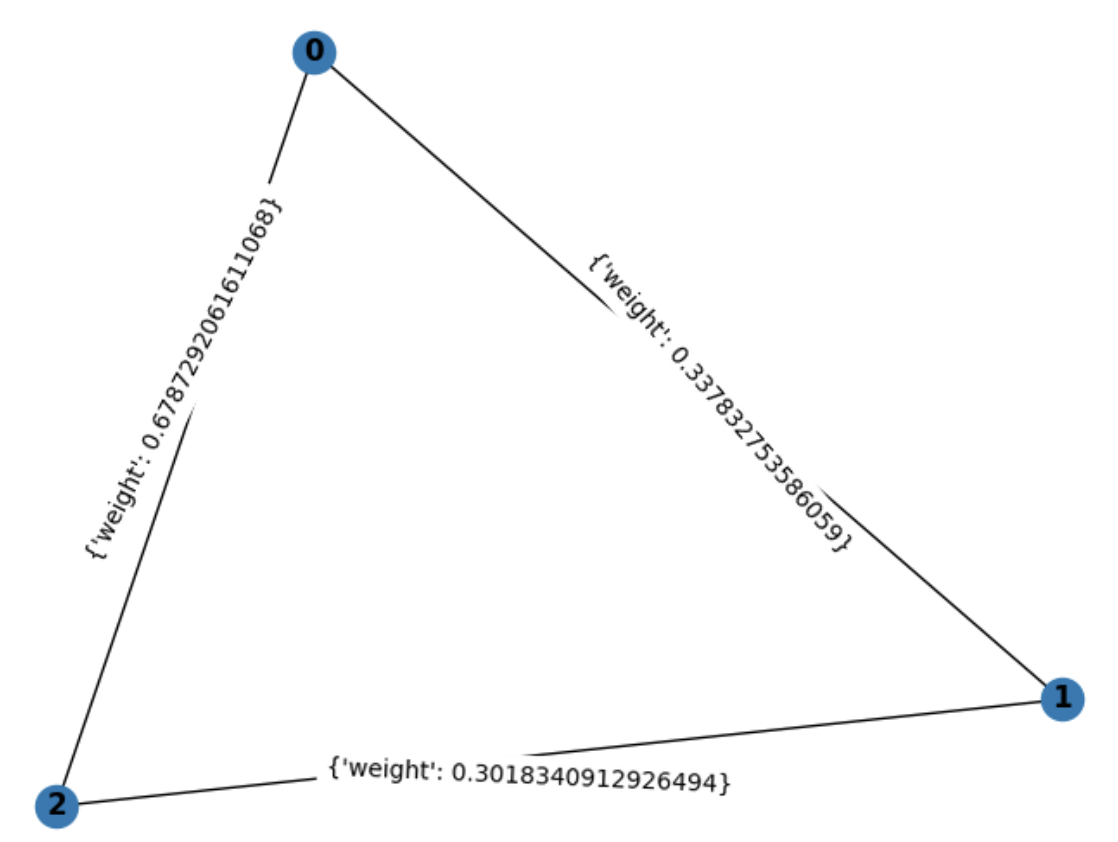
The edges (0,1) and (1,2) connects all nodes in the graph, and picking these edges minimizes the total weight of the tree. If all the weights in an undirected weighted graph are unique, then the MST is also unique, meaning everyone will find the same MST for a given graph.

Write a program implementing another example of a greedy algorithm to find the MST. Several algorithms solve this problem, but Prim's algorithmLinks to an external site. is likely the easiest to implement.

Input format

Your program should take a single command line argument specifying the path to an input file. Test cases for your program are in the tests/ directory. In each test case, the first line records the number of nodes N in the graph. Then, the adjacency matrix is recorded in the subsequent N rows of the file. This time, the adjacency matrix contains floating point numbers. 0.0 indicates no edge between two nodes. Any other value indicates an edge with the given value as the edge weight.

Output format

Expected outputs from your program for each test case are in the answers/ directory. You should print a list of edges that, taken together, form the MST of the input graph. Again, the ordering of the nodes in each edge does not matter. The ordering of the edges does not matter.

Example input: reads txt from file:

5

0.0 0.7309552626846215 0.046025649869375296 0.8211470163786211 0.49582048891999064

0.7309552626846215 0.0 0.18528476143252726 0.12309567426737433 0.8800946960775891

0.046025649869375296 0.18528476143252726 0.0 0.8459419457234398 0.7790333431240075

0.8211470163786211 0.12309567426737433 0.8459419457234398 0.0 0.02163102133759487

0.49582048891999064 0.8800946960775891 0.7790333431240075 0.02163102133759487 0.0

Ouput:

0 2

1 3

1 2

3 4

graphutils.h

#include

#include

#include

#include

#include

#include

typedefsize_tgraphNode_t;

typedefstructAdjacencyListNode AdjacencyListNode;

structAdjacencyListNode {

graphNode_t graphNode; //the destination graph node

doubleweight; //a weight, if weighted graph, otherwise will be 1.0

AdjacencyListNode* next; //pointer to next linked list node

};

boolalmostEqual(doublea, doubleb)

{

returnfabs(a - b)

}

//READ INPUT FILE TO CREATE GRAPH ADJACENCY LIST

//Reads adjacency matrices for both undirected and directed graphs.

//Reads adjacency matrices for both unweighted and weighted graphs.

//Returns the number of nodes in the graph; returns 0 if reading failed.

size_tadjMatrixToList(

constchar* filename, //path to input file containing adjacency matrix

AdjacencyListNode** adjacencyList

) {

FILE* fp = fopen(filename, "r");

if(!fp) {

perror("fopen failed");

return0;

}

//first, read the graphNodeCount

size_tgraphNodeCount;

fscanf(fp, "%ld", &graphNodeCount);

/ext, allocate the linked list heads

*adjacencyList = calloc( graphNodeCount, sizeof(AdjacencyListNode) );

//finally, read the adjacency matrix and allocate linked list nodes

for(size_tadjMatrixRow=0; adjMatrixRow

(*adjacencyList)[adjMatrixRow].graphNode= adjMatrixRow; //A note indicating source graph node

(*adjacencyList)[adjMatrixRow].next= NULL;

for(size_tadjMatrixCol=0; adjMatrixCol

doubleweight;

fscanf(fp, "%lf", &weight);

if( !almostEqual(weight,0.0) ) { //if not almost zero, indicating an edge exists

AdjacencyListNode* newTop = calloc(1,sizeof(AdjacencyListNode));

newTop->graphNode= adjMatrixCol;

newTop->weight= weight;

newTop->next= (*adjacencyList)[adjMatrixRow].next;

(*adjacencyList)[adjMatrixRow].next= newTop;

}

}

}

fclose(fp);

returngraphNodeCount;

}

//TRAVERSE AND FREE THE LINKED LISTS, AND FREE THE ADJACENCY LIST

voidfreeAdjList(

size_tgraphNodeCount,

AdjacencyListNode* adjacencyList

) {

//example of how to traverse the graph adjacency list

for(size_tsource=0; source

AdjacencyListNode* dest = adjacencyList[source].next;

//list iterator

while(dest) {

AdjacencyListNode* temp = dest;

dest = dest->next; //iterator moves to next

free(temp);

}

}

free(adjacencyList);

}

Edit the given code below:

#include "../graphutils.h" // header for functions to load and free adjacencyList

// A program to find the minimum spanning tree of a weighted undirected graph using Prim's algorithm

int main ( int argc, char* argv[] ) {

// READ INPUT FILE TO CREATE GRAPH ADJACENCY LIST

AdjacencyListNode* adjacencyList;

/* ... */

// An array that keeps track of who is the parent node of each graph node we visit

// In Prim's algorithm, this parents array keeps track of what is the edge that connects a node to the MST.

graphNode_t* parents = calloc( graphNodeCount, sizeof(graphNode_t) );

for (size_t i=0; i

parents[i] = -1; // -1 indicates that a nodes is not yet visited; i.e., node not yet connected to MST.

}

graphNode_t root = rand()%graphNodeCount;

parents[root] = root;

// Prim's algorithm:

// A greedy algorithm that builds the minimum spanning tree.

// For a graph with N nodes, the minimum spanning tree will have N-1 edges spanning all nodes.

// Prim's algorithm starts with all nodes unconnected.

// At each iteration of Prim's algorithm, the minimum weight node that connects an unconnected node to the connected set of nodes is added to the MST.

for (unsigned iter=0; iter

double minWeight = DBL_MAX; // If we find an edge with weight less than this minWeight, and edge connects a new node to MST, then mark this as the minimum weight to beat.

graphNode_t minSource = -1;

graphNode_t minDest = -1;

for (graphNode_t source=0; source

if (parents[source]!=-1) { // if already visited

/* ... */

}

}

parents[minDest]=minSource; // we found the minimum weight

}

// Using the fully populated parents array, print the edges in the MST.

/* ... */

free (parents);

freeAdjList ( graphNodeCount, adjacencyList );

return EXIT_SUCCESS;

}

And this is its MST