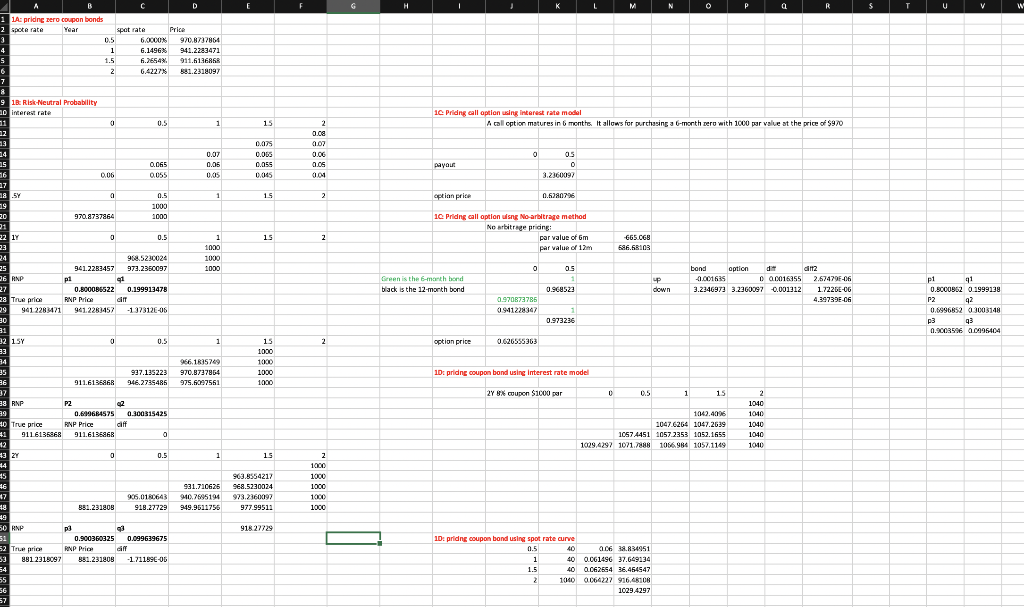
This is the Question and solution, I just have a doubt that how is the par value of 6m and 12m is calculated in 1C No arbitrage method. Please show calculations.

1. Constructing a risk-neutral probability binomial short-term interest rate model (40 points) 1a. We observe the following spot rate curve. Assume semiannual compounding and $1000 par value. Calculate the prices of 0.5y, ly, 1.5y, and 2y zero-coupon Treasury bonds. period 2 3 Years 0.5 1 1.5 2 Annualized Spot Rate 6.0000% 6.1496% 6.2654% 6.4227% 1b. The binomial tree of the annualized 6-month short-term interest rate is in the table below. Each period represents a six-month time interval. Find the risk-neutral probability pl under which the binomial tree model prices the 1-year zero-coupon bond correctly. Once we know pl, find the risk-neutral probability p2 such that the risk-neutral binomial tree model prices the 1.5-year zero- coupon bond correctly. Last, when we know pl and p2,, find the risk-neutral probability p3 such that the risk-neutral binomial tree model prices the 2-year zero-coupon bond correctly. 1 2 3 p3 p2 7.5% pl 7% 6.5% 1-p3 6.5% 6% 1-p26% 5.5% 5.5% 1-pl 5% 4.5% 1c. There is a call option with 6-month expiration. The call option allows you to purchase a 6- month zero-coupon bond with $1000 par value at the price of $970 in the next period. Price the call option using the risk-neutral binomial tree that you developed in lb. Construct a bond portfolio of 0.5Y and 1Y zero-coupon bonds such that the bond portfolio has cash flows identical to those of the call option. Verify that the price of the bond portfolio is identical to the price of the call option 1 1d. There is a 2-year 8% coupon bond with the par value of $1000. Price the bond using (1) the spot rate curve provided in 1a and the risk-neutral binomial tree developed in 1b. Verify that prices obtained from the two methods are identical. G H K M N P Q R S T U V W C D 1A: pridne zero coupon bonds 2 spote rate Year spot rate Price 3 0.5 6.0000 970.8737864 4 1 G.1496 941.2283471 5 1.5 6.2654 911.616 2 6.4227 581.2318097 7 8 9 1B: Risk Neutral Probability 20 interest rate 11 0 0.5 1 53 10. Priding call option using interest rate model A call option matures in 6 months. It allows for purchasing a 6-month pero with 1000 par value at the price of $970 15 2 o.ca 0.07 0 OS 0.02s 0.OBS 0.055 0.45 0.07 0.05 0.25 as 16 0.065 0055 0.05 001 payout 0.06 3.2360097 - 1 15 2 option price 0.5280796 10 Pridng call option ulang No-arbitrage method Ne arbitrage pridng : par value of Gm par value of 1 15 2 2 665.068 586.58103 8 a 0.5 1000 20 970.8737864 1000 21 22 1 0 0.5 23 24 968.5230024 25 941.2283457 973.2350097 26 RNP pl 1 27 0.800086522 0.199913478 28 True price RNP Price cim 29 901 228421 9612283-157 -1 37312-06 30 1 1000 1000 1000 0 OS Green is the 6-month bond black is the 12-month bond up down bond option dit dit2 -0.001635 0 0.0016958 2.67479F-0. 3.2346973 3.2360097 0.001312 1.72260-06 4.39739E-06 0.968523 9.970873786 0941228307 p1 91 0.5000862 0.1999100 P2 42 0.6996852 3003148 p3 93 0.9003506 2.0995404 0.973236 1 2 option price 0.626556363 966.183576 970.8737864 975.6097561 15 1000 1000 1000 1000 10: pridng coupon band using interest rate model 32 15Y 0 0.5 33 34 35 937.15223 BE 911.613586 346.2795486 37 22 38 RNP P2 02 39 0.689684575 0.300315425 10 True price RNP Price cilt 9116125868 911.6136868 0 27 8x coupon Sicou por D 0.5 1 15 1042.4096 1047.6264 1047.2639 1057 4451 1057.2353 1052.1655 1029.4297 1071.7888 1056,986 1057.1149 2 1040 1010 1040 1040 1010 13 ZY 0 0.5 1 15 931.710626 20.7695194 949.9511756 963.8554217 968.5230024 923.2160097 977.99511 2 1000 1000 1000 1000 1000 = 45 46 905.0160643 381.231808 918.27729 49 50 ANP p3 3 51 0.900360325 0.099639675 52 True price PNP Price cil 53 9812315097 381.231909 -1.71159E-OG 91827229 a 1D: pridng coupon band using spot rate curve 0.5 40 0.06 38.834951 1 40 0.061496 37.649134 1.5 40 0.062594 36.464547 2 1KO 0.064227 916.48108 1029.4297 55 56 1. Constructing a risk-neutral probability binomial short-term interest rate model (40 points) 1a. We observe the following spot rate curve. Assume semiannual compounding and $1000 par value. Calculate the prices of 0.5y, ly, 1.5y, and 2y zero-coupon Treasury bonds. period 2 3 Years 0.5 1 1.5 2 Annualized Spot Rate 6.0000% 6.1496% 6.2654% 6.4227% 1b. The binomial tree of the annualized 6-month short-term interest rate is in the table below. Each period represents a six-month time interval. Find the risk-neutral probability pl under which the binomial tree model prices the 1-year zero-coupon bond correctly. Once we know pl, find the risk-neutral probability p2 such that the risk-neutral binomial tree model prices the 1.5-year zero- coupon bond correctly. Last, when we know pl and p2,, find the risk-neutral probability p3 such that the risk-neutral binomial tree model prices the 2-year zero-coupon bond correctly. 1 2 3 p3 p2 7.5% pl 7% 6.5% 1-p3 6.5% 6% 1-p26% 5.5% 5.5% 1-pl 5% 4.5% 1c. There is a call option with 6-month expiration. The call option allows you to purchase a 6- month zero-coupon bond with $1000 par value at the price of $970 in the next period. Price the call option using the risk-neutral binomial tree that you developed in lb. Construct a bond portfolio of 0.5Y and 1Y zero-coupon bonds such that the bond portfolio has cash flows identical to those of the call option. Verify that the price of the bond portfolio is identical to the price of the call option 1 1d. There is a 2-year 8% coupon bond with the par value of $1000. Price the bond using (1) the spot rate curve provided in 1a and the risk-neutral binomial tree developed in 1b. Verify that prices obtained from the two methods are identical. G H K M N P Q R S T U V W C D 1A: pridne zero coupon bonds 2 spote rate Year spot rate Price 3 0.5 6.0000 970.8737864 4 1 G.1496 941.2283471 5 1.5 6.2654 911.616 2 6.4227 581.2318097 7 8 9 1B: Risk Neutral Probability 20 interest rate 11 0 0.5 1 53 10. Priding call option using interest rate model A call option matures in 6 months. It allows for purchasing a 6-month pero with 1000 par value at the price of $970 15 2 o.ca 0.07 0 OS 0.02s 0.OBS 0.055 0.45 0.07 0.05 0.25 as 16 0.065 0055 0.05 001 payout 0.06 3.2360097 - 1 15 2 option price 0.5280796 10 Pridng call option ulang No-arbitrage method Ne arbitrage pridng : par value of Gm par value of 1 15 2 2 665.068 586.58103 8 a 0.5 1000 20 970.8737864 1000 21 22 1 0 0.5 23 24 968.5230024 25 941.2283457 973.2350097 26 RNP pl 1 27 0.800086522 0.199913478 28 True price RNP Price cim 29 901 228421 9612283-157 -1 37312-06 30 1 1000 1000 1000 0 OS Green is the 6-month bond black is the 12-month bond up down bond option dit dit2 -0.001635 0 0.0016958 2.67479F-0. 3.2346973 3.2360097 0.001312 1.72260-06 4.39739E-06 0.968523 9.970873786 0941228307 p1 91 0.5000862 0.1999100 P2 42 0.6996852 3003148 p3 93 0.9003506 2.0995404 0.973236 1 2 option price 0.626556363 966.183576 970.8737864 975.6097561 15 1000 1000 1000 1000 10: pridng coupon band using interest rate model 32 15Y 0 0.5 33 34 35 937.15223 BE 911.613586 346.2795486 37 22 38 RNP P2 02 39 0.689684575 0.300315425 10 True price RNP Price cilt 9116125868 911.6136868 0 27 8x coupon Sicou por D 0.5 1 15 1042.4096 1047.6264 1047.2639 1057 4451 1057.2353 1052.1655 1029.4297 1071.7888 1056,986 1057.1149 2 1040 1010 1040 1040 1010 13 ZY 0 0.5 1 15 931.710626 20.7695194 949.9511756 963.8554217 968.5230024 923.2160097 977.99511 2 1000 1000 1000 1000 1000 = 45 46 905.0160643 381.231808 918.27729 49 50 ANP p3 3 51 0.900360325 0.099639675 52 True price PNP Price cil 53 9812315097 381.231909 -1.71159E-OG 91827229 a 1D: pridng coupon band using spot rate curve 0.5 40 0.06 38.834951 1 40 0.061496 37.649134 1.5 40 0.062594 36.464547 2 1KO 0.064227 916.48108 1029.4297 55 56