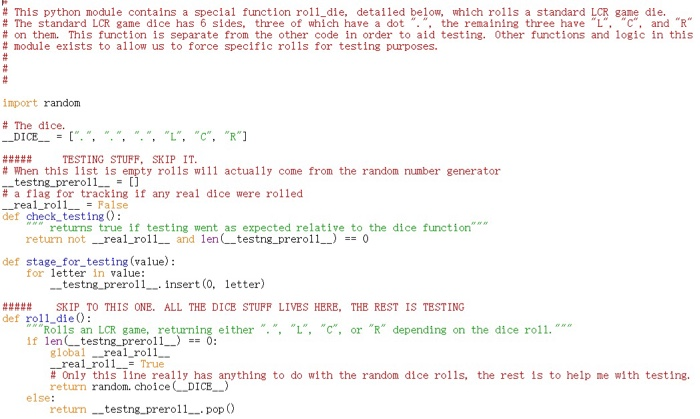
# This python module contains a special function roll_die, detailed below, which rolls a standard LCR game die. # The standard LCR game dice has 6 sides, three of which have a dot ".". the remaining three have "L", "C" and "R" # on them. This function is separate from the other code in order to aid testing. Other functions and logic in this # module exists to allow us to force specific rolls for testing purposes. import random # The dice. _DICE_2=1".", ".",".", "1", "c", "r"] ##### TESTING STUFF. SKIP IT. # When this list is empty rolls will actually come from the random number generator -testng preroll_ = [] # a flag for tracking if any real dice were rolled __real_roll__ = False def check_testing(): "returns true if testing went as expected relative to the dice function return not __real_roll__ and len__testng_prero11_) == 0 def stage_for_testing (value): for letter in value: _testng preroll__ insert(0, letter) ##### SKIP TO THIS ONE. ALL THE DICE STUFF LIVES HERE, THE REST IS TESTING def roll die(): **"Rolls an LCR game, returning either".", "1", "C", or "R" depending on the dice roll.**** if len(_testng_preroll__) == 0: global __real_roll__ __real_ro11__ = True # Only this line really has anything to do with the random dice rolls, the rest is to help me with testing. return random. choice DICE_) else: return __testng preroll_pop LCR (short for "left right center") is a game largely focused around the movement of "coins" (poker chips, candy, money, whatever) around the players. Each turn the active player rolls dice to determine how to move their coins either keeping them, putting them in the center, or passing the left or right. The goal of the game is to be the only player with coins, at which point that player wins the coins they have and all coins in the center. The game is played with special 6-sided dice, three sides are labeled with a dot, representing that a coin can be kept, then one side each is labeled L (left), R (right) and C (center). It is from these dice that the game gets it's name. At the beginning of the game, the players sit in a circle, each with three coins. One player is chosen to go first, afterwords play will go in a circle until the game completes. A player's turn has three parts. First the player figures out how many dice they must roll. The player rolls as many dice as they have coins, capped at a maximum of three dice. So, if a player has three of fewer coins, they roll as many dice as they have coins, but if they have four or more coins, they would only roll three dice. Then the player rolls their dice. For each dice that rolls an L the player must hand a coin to the player on their left. For each dice that rolls an R the player must hand a coin to the player on their right. For each dice that rolls a C the player must put a coin the center, coins in the center cannot be retrieved until the end of the game. If a dice rolls a dot, the player doesn't have to give up a coin. If a player has no coins they are still in the game, but they roll no dice on their turn and nothing happens. (For our purposes, we will still count that as a turn, even though nothing happens) These player stay in the game because the player to their left or right may still be forced to give them coins. The game ends when only one player has coins. This can happen on anyone's turn (so player 1 can be declared a winner at the beginning of player 3's turn, if no other player has coins). There are many variants of this game, some of which add strategy (which I feel this game is sorely lacking, no one asked me). We will not be simulating those games, however, only the basic game. The major data that needs to be recorded about this game is how many coins each player has. The number of players is not fixed (it won't change as the game goes on, but we may want to simulate the game at different sizes so we can't just use one variable for each player), and the number of coins any player has will change. Therefore we will represent this count with a list of numbers, with each element of the list representing that player's coin count. Likewise we will need to track whose turn it is currently. Since we are using a list to track coin counts, it is only natural to track players by their index. We will assume that player 0 always goes first this is somewhat contrary to normal rules for the game). We will assume that "left" goes to the index one lower, and "right" goes to the index one higher, and that play goes to the right (so player/index 0 goes first, then player 1, then player 2 and so forth until it circles around to 0) Note that this assumption means for N players (numbered 0 though N - 1) player N - 1 is left of player 0 and player 0 is right of player N - 1. We will represent the LCR dice with a function the returns "L", "C", "R", or "." with appropriate probabilities. This function is provided. Since we are not interested in the "winnings" of any given player, only who wins, we will not be recording the number of coins in the center. This data representation is useful as it essentially reduces the game to a series of list manipulations, and allows us to track all information about the state of a game-in-progress with only two variables: the list of coin counts, and the current player's index. 8 Requirements and software design While I would love to leave you at this point, give you design freedom, and see what you build, that would be better suited as a Project than a Lab. Therefore, and for the sake of testing) I've gone ahead and reduced this application to a series of simple functions. All the functions listed here are required, but you are free to write other useful functions. Each of these functions has at least two tests in the testing file provided on canvas. To use that test file you MUST name your python module lor_sim.py krover(coins) this function takes an array of numbers (representing coin counts) and indicates if the game is over that is, it returns true if only one clement is non-zero, and false if more than one element is non-zero) Irwinner(coins) this function takes an array of numbers (representing coin counts). You can assume that this function is only called when there is a winner, that is, this function will only be called if l over(coins) returns true. This function should return the index of the player who won the game. That is, this function should return the index of the non-zero element of the coins list. left (coins, player) this function takes two parameters, the coins list, and the index of the current player. It should perform a "left" on that player's coin count, reducing it by one, and increasing the player to the left's coin count by one. Remember, as players sit in a circle, left of the first player is the last" player. This function should return nothing, it should instead directly change the list. right(coins, player) like left, but performing a right shift, so removing one coin from player and giving it to the player to the right. This function should return nothing center(coins, player) like left and right, but with the coin going to the center As we don't track coins in the center, this just needs to reduce the coin count for player by one. . Ir game muam.players) this function should simulate to completion, a game of ler. It should start with each player having 3 coins, and player 0 going first, and it should continue until only one player has coins per the rules of the game discussed above. This function should return a tuple with two values, the first value in the tuple is the index of the player who won. The second value should be the number of turns it took to win . most.common winner(num.players) This function should simulate 2000 games with the given number of players. It should count how many times each player wins, and then figure out which player won the most over the 2000 games. This function should return a tuple with two values. The first value is the player who won the most of the simulated 2000 games. The second value is the percent of those games the player won (so win.count/2000). This function is the end goal of our program, it will tell us if the game is fair, and if not, how often a given player wins. This function should run relatively quickly (maximum one or two seconds) # This python module contains a special function roll_die, detailed below, which rolls a standard LCR game die. # The standard LCR game dice has 6 sides, three of which have a dot ".". the remaining three have "L", "C" and "R" # on them. This function is separate from the other code in order to aid testing. Other functions and logic in this # module exists to allow us to force specific rolls for testing purposes. import random # The dice. _DICE_2=1".", ".",".", "1", "c", "r"] ##### TESTING STUFF. SKIP IT. # When this list is empty rolls will actually come from the random number generator -testng preroll_ = [] # a flag for tracking if any real dice were rolled __real_roll__ = False def check_testing(): "returns true if testing went as expected relative to the dice function return not __real_roll__ and len__testng_prero11_) == 0 def stage_for_testing (value): for letter in value: _testng preroll__ insert(0, letter) ##### SKIP TO THIS ONE. ALL THE DICE STUFF LIVES HERE, THE REST IS TESTING def roll die(): **"Rolls an LCR game, returning either".", "1", "C", or "R" depending on the dice roll.**** if len(_testng_preroll__) == 0: global __real_roll__ __real_ro11__ = True # Only this line really has anything to do with the random dice rolls, the rest is to help me with testing. return random. choice DICE_) else: return __testng preroll_pop LCR (short for "left right center") is a game largely focused around the movement of "coins" (poker chips, candy, money, whatever) around the players. Each turn the active player rolls dice to determine how to move their coins either keeping them, putting them in the center, or passing the left or right. The goal of the game is to be the only player with coins, at which point that player wins the coins they have and all coins in the center. The game is played with special 6-sided dice, three sides are labeled with a dot, representing that a coin can be kept, then one side each is labeled L (left), R (right) and C (center). It is from these dice that the game gets it's name. At the beginning of the game, the players sit in a circle, each with three coins. One player is chosen to go first, afterwords play will go in a circle until the game completes. A player's turn has three parts. First the player figures out how many dice they must roll. The player rolls as many dice as they have coins, capped at a maximum of three dice. So, if a player has three of fewer coins, they roll as many dice as they have coins, but if they have four or more coins, they would only roll three dice. Then the player rolls their dice. For each dice that rolls an L the player must hand a coin to the player on their left. For each dice that rolls an R the player must hand a coin to the player on their right. For each dice that rolls a C the player must put a coin the center, coins in the center cannot be retrieved until the end of the game. If a dice rolls a dot, the player doesn't have to give up a coin. If a player has no coins they are still in the game, but they roll no dice on their turn and nothing happens. (For our purposes, we will still count that as a turn, even though nothing happens) These player stay in the game because the player to their left or right may still be forced to give them coins. The game ends when only one player has coins. This can happen on anyone's turn (so player 1 can be declared a winner at the beginning of player 3's turn, if no other player has coins). There are many variants of this game, some of which add strategy (which I feel this game is sorely lacking, no one asked me). We will not be simulating those games, however, only the basic game. The major data that needs to be recorded about this game is how many coins each player has. The number of players is not fixed (it won't change as the game goes on, but we may want to simulate the game at different sizes so we can't just use one variable for each player), and the number of coins any player has will change. Therefore we will represent this count with a list of numbers, with each element of the list representing that player's coin count. Likewise we will need to track whose turn it is currently. Since we are using a list to track coin counts, it is only natural to track players by their index. We will assume that player 0 always goes first this is somewhat contrary to normal rules for the game). We will assume that "left" goes to the index one lower, and "right" goes to the index one higher, and that play goes to the right (so player/index 0 goes first, then player 1, then player 2 and so forth until it circles around to 0) Note that this assumption means for N players (numbered 0 though N - 1) player N - 1 is left of player 0 and player 0 is right of player N - 1. We will represent the LCR dice with a function the returns "L", "C", "R", or "." with appropriate probabilities. This function is provided. Since we are not interested in the "winnings" of any given player, only who wins, we will not be recording the number of coins in the center. This data representation is useful as it essentially reduces the game to a series of list manipulations, and allows us to track all information about the state of a game-in-progress with only two variables: the list of coin counts, and the current player's index. 8 Requirements and software design While I would love to leave you at this point, give you design freedom, and see what you build, that would be better suited as a Project than a Lab. Therefore, and for the sake of testing) I've gone ahead and reduced this application to a series of simple functions. All the functions listed here are required, but you are free to write other useful functions. Each of these functions has at least two tests in the testing file provided on canvas. To use that test file you MUST name your python module lor_sim.py krover(coins) this function takes an array of numbers (representing coin counts) and indicates if the game is over that is, it returns true if only one clement is non-zero, and false if more than one element is non-zero) Irwinner(coins) this function takes an array of numbers (representing coin counts). You can assume that this function is only called when there is a winner, that is, this function will only be called if l over(coins) returns true. This function should return the index of the player who won the game. That is, this function should return the index of the non-zero element of the coins list. left (coins, player) this function takes two parameters, the coins list, and the index of the current player. It should perform a "left" on that player's coin count, reducing it by one, and increasing the player to the left's coin count by one. Remember, as players sit in a circle, left of the first player is the last" player. This function should return nothing, it should instead directly change the list. right(coins, player) like left, but performing a right shift, so removing one coin from player and giving it to the player to the right. This function should return nothing center(coins, player) like left and right, but with the coin going to the center As we don't track coins in the center, this just needs to reduce the coin count for player by one. . Ir game muam.players) this function should simulate to completion, a game of ler. It should start with each player having 3 coins, and player 0 going first, and it should continue until only one player has coins per the rules of the game discussed above. This function should return a tuple with two values, the first value in the tuple is the index of the player who won. The second value should be the number of turns it took to win . most.common winner(num.players) This function should simulate 2000 games with the given number of players. It should count how many times each player wins, and then figure out which player won the most over the 2000 games. This function should return a tuple with two values. The first value is the player who won the most of the simulated 2000 games. The second value is the percent of those games the player won (so win.count/2000). This function is the end goal of our program, it will tell us if the game is fair, and if not, how often a given player wins. This function should run relatively quickly (maximum one or two seconds)