This question asks you to price and describe the replicating portfolio for options on a non-dividend-paying stock whose price is currently $16. The price evolves on a binomial tree as follows:

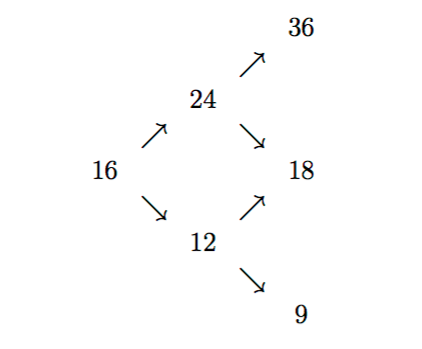
The time interval between each stage is h = 6 months (ie, six months from today the price will be either 24 or 12; six months later, it will be either 36, 18, or 9). The discretely compounded six-month rate is 5.127%.

1. What is the risk-neutral probability of an upward price move, q?

2. Find the price of the following options:

   i. An at-the-money European call expiring in 6 months. ii. A European call with strike 17, expiring in 1 year.

   iii. An American call with strike 17, expiring in 1 year. iv. A European put with strike 17, expiring in 1 year.

   v. An American put with strike 17, expiring in 1 year

3. Find the delta, at each point in time, of the last two options in the previous part You sell a 1-year European put with strike 17 to a customer at mid-market, assuming the above binomial tree, and hedge appropriately. Six months pass and volatility suddenly rises: you now realize that the price will either double or halve. (So, if the price is 24 after six months, it will now go to either 12 or 48 after a further six months; if the price is 12 after six months, it will go to either 24 or 6.) What effects does this have on your position? Be specific: think about things like how your desired hedge changes, and the effect on your P&L.

Bok or sta as k Bok or sta as k