Answered step by step
Verified Expert Solution
Question
1 Approved Answer
This question is a assignment of Linear Algebra, especially about Singular value decomposition. Professor said AA T 's eigenvectors are column vectors of U matrix,
This question is a assignment of Linear Algebra, especially about "Singular value decomposition". Professor said "AAT's eigenvectors are column vectors of U matrix", but I'm not sure that should I use this. sigma is an r x r diagonal matrix whose diagonal entries are the nonzero singular values. V is a matrix that's column vectors are eigenvector of A. Following picture is about U matrix.
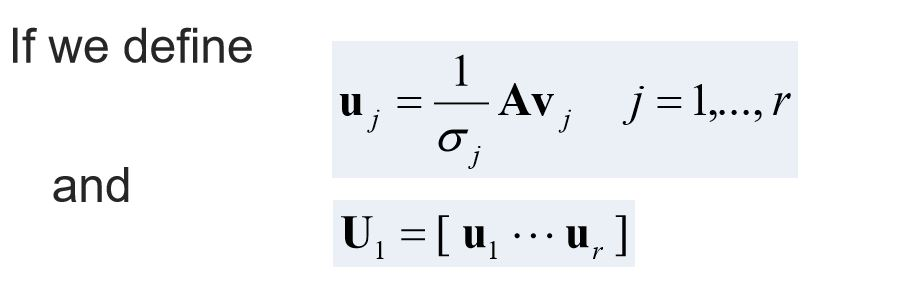

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


