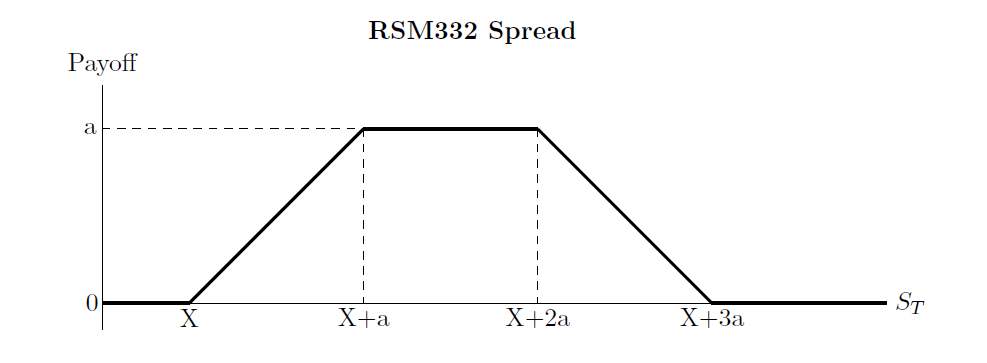
(This question is to be solve algebraically)

3. A RSM332 spread is a combination of option positions that involves four strike prices (see figure below, which shows the gross payoffs). For this problem, assume that the options are European with the same maturity and that a > 0. 1. Find the option positions and strike prices necessary to obtain the RSM332 spread. Show that your portfolio replicates the spread payoff and assume that the underlying options are all call options. 2. Find the option positions and strike prices necessary to obtain the RSM332 spread. Show that your portfolio replicates the spread payoff and assume that the underlying options are all put options. 3. Consider the following strategy: (i) buy a call with a strike price of X, and (ii) buy a put with a strike price of X+3a. Assuming no arbitrage, show mathematically that the initial investment (i.e. the amount of money you need to pay at t=0) to create the strategy is higher than the initial investment to create the RSM332 spread. RSM332 Spread Payoff a ---- - - - - - - - - - - - - - - - ST X+a X+2a X+3a 3. A RSM332 spread is a combination of option positions that involves four strike prices (see figure below, which shows the gross payoffs). For this problem, assume that the options are European with the same maturity and that a > 0. 1. Find the option positions and strike prices necessary to obtain the RSM332 spread. Show that your portfolio replicates the spread payoff and assume that the underlying options are all call options. 2. Find the option positions and strike prices necessary to obtain the RSM332 spread. Show that your portfolio replicates the spread payoff and assume that the underlying options are all put options. 3. Consider the following strategy: (i) buy a call with a strike price of X, and (ii) buy a put with a strike price of X+3a. Assuming no arbitrage, show mathematically that the initial investment (i.e. the amount of money you need to pay at t=0) to create the strategy is higher than the initial investment to create the RSM332 spread. RSM332 Spread Payoff a ---- - - - - - - - - - - - - - - - ST X+a X+2a X+3a