this sodo code Convert it to c++ code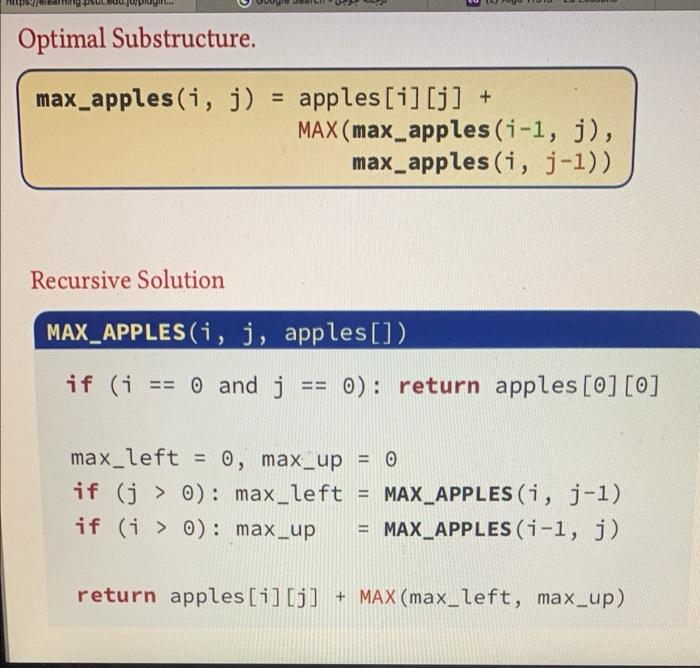

Optimal Substructure. \[ \begin{array}{l} \text { max_apples }(i, j)=\operatorname{apples}[i][j]+ \\ \text { MAX (max_apples }(i-1, j) \text {, } \\ \text { max_apples }(i, j-1)) \\ \end{array} \] Recursive Solution MAX_APPLES (i,j, apples [] ) if (i==0 and j==0) : return apples [0] [0] max_left =0, max_up =0 if (j>0) : max_left = MAX_APPLES (i,j1) if (i>0): max_up =MAXAPPLES(i1,j) return apples[i][j] + MAX(max_left, max_up)