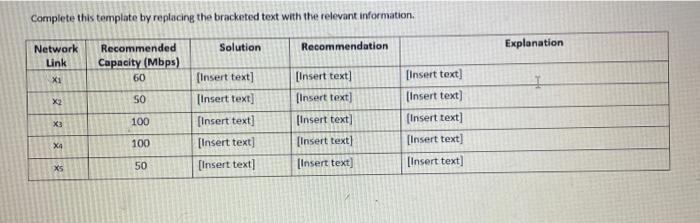
To complete the project, work on the problems described below. As you complete each part, show your work and carefully describe how you arrive at your final answer. The methods and conclusions need to be clear when sharing your results with management. Any MATLAB code or MATLAB terminal outputs you generate should be provided in your submitted document to support your answers and work. 1. Develop a system of linear equations for the network by writing an equation for each router (A, B, C, D, and E. Make sure to write your final answer as Ax=b where A is the 55 coefficient matrix, x is the 51 vector of unknowns, and b is a 51 vector of constants. 2. Use MATLAB to construct the augmented matrix [Ab] and then perform row reduction using the rref0 function. Write out your reduced matrix and identify the free and basic variables of the system. 3. Use MATLAB to compute the LU decomposition of A, L.e. find A=LU. For this decomposition, find the transformed set of equations Ly=b. Solve the system of equations Ly=b for the unknown vector y. 4. Use MATLAB to compute the inverse of U using the inv0 function. 5. Compute the solution to the original system of equations by transforming y into x, Le. compute xy i y. 6. Check your answer for Tri using Cramer's Rule. 7. Use MATLAB to compute the required determinants using the det0 function. The Project One Table Terrplate, provided in the Supporting Materials section, shows the recommended throughput capacity of each link in the network Put your solution for the system of equations in the third column so it can be easily compared to the maximum capacity in the second columin in the fourth column of the table. provide recommendations for how the network should be modified based on your network throughput analysis findings. The modification options can be No Change. Remove Link, or Uprade Link in the final column, explain how you arrived at your recommendation. Complete this template by replacing the bracketed text with the relevant information. Problem 1 Solutitien Problem 2 Sollution: Problem 3 Solution: (tran Problem 4 Solution: Problem 5 Solution: Metalr Problem 6 Solution: Problem 7 50 istion