To test whether the mean time needed to mix a batch of material is the same for machines produced by three manufacturers, a chemical company obtained the following data on the time (in minutes) needed to mix the material.

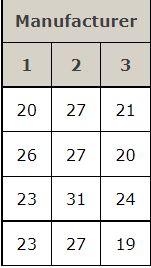
a)

Use these data to test whether the population mean times for mixing a batch of material differ for the three manufacturers. Use

= 0.05.

State the null and alternative hypotheses.

H₀: Not all the population means are equal. H_a: ₁ = ₂ = ₃

H₀: ₁ = ₂ = ₃ H_a: _{1 2 3}

H₀: ₁ = ₂ = ₃ H_a: Not all the population means are equal.

H₀: _{1 2 3} H_a: ₁ = ₂ = ₃

H₀: At least two of the population means are equal. H_a: At least two of the population means are different.

Find the value of the test statistic. (Round your answer to two decimal places.)

Find the p-value. (Round your answer to three decimal places.)

p-value =

State your conclusion.

Do not reject H₀. There is not sufficient evidence to conclude that the mean time needed to mix a batch of material is not the same for each manufacturer.

Reject H₀. There is not sufficient evidence to conclude that the mean time needed to mix a batch of material is not the same for each manufacturer.

Reject H₀. There is sufficient evidence to conclude that the mean time needed to mix a batch of material is not the same for each manufacturer.

Do not reject H₀. There is sufficient evidence to conclude that the mean time needed to mix a batch of material is not the same for each manufacturer.

(b)

At the = 0.05 level of significance, use Fisher's LSD procedure to test for the equality of the means for manufacturers 1 and 3.

Find the value of LSD. (Round your answer to two decimal places.)

LSD =

Find the pairwise absolute difference between sample means for manufacturers 1 and 3.

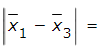
What conclusion can you draw after carrying out this test?

There is a significant difference between the means for manufacturer 1 and manufacturer 3.

There is not a significant difference between the means for manufacturer 1 and manufacturer 3.

Manufacturer \begin{tabular}{|c|c|c|} \hline 1 & 2 & 3 \\ \hline 20 & 27 & 21 \\ \hline 26 & 27 & 20 \\ \hline 23 & 31 & 24 \\ \hline 23 & 27 & 19 \\ \hline \end{tabular} x1x3=