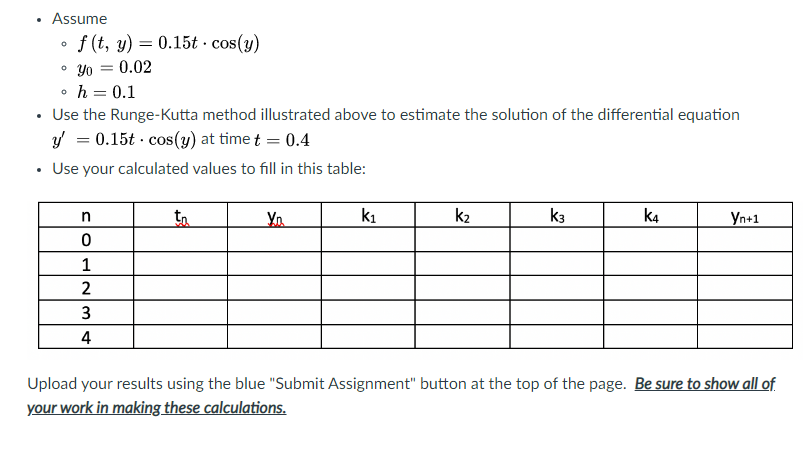
To this point in MTHZEDXSED, we have been learning the mechanics of differentiation and integration, along with some realworld applications. But by far the most important application of calculus is dl'erenai equations. Differential equations are simply equations involving derivatives; and they are solved using various integration techniques. Differential equations are important because they allow us to accurately model dynamic systems. That is, a differential equation describes how quickly a certain variable is changing with respect to time; and if we also happen to know that variable's initial value, the differential equation allows us to predict its value at any subsequent time. There are many different forms of differential equations; and mathematicians, physicists. and engineers have spent much of the last three centuries trying to solve them. In some elementary cases, we can derive an exact solution that is valid for any time t in the future; and you'll encounter several of these in your Math XL Homework assignments. But most differential equations are too complex to solve, including the NavierStokes equation that models fluid ow, used for everything from aerodynamical design to weather forecasting. Rather than a full and exact solution, we can only use numerical methods to estimate the solution. Among the most important numerical methods are the RungeKutta methods. In this exercise, we will use one of these methods to estimate the solution to a differential equation. Specically, let's say that the differential equation can be written in the form yr : fury} That is, the derivative of y is a function of both time f, and the actual function y itself. We also assume that we know the initial condition y [to] = ya. Dur objective is to approximate the value of y at time t = t5 . We select a stepsize of time, which we'll represent by h. Starting at time t = 0. our strategy will be to move toward one step-size at a time solving for the approximate value of the function y (t) at that time step. then using that most recent approximation as the basis for taking our next time step. We will continue that process until we reach time tc , at which point we'll stop. To state the algorithm in its most general form. we dene time step n+1 as ind1 = in + h Knowing the approximate solution y\" at time step in . we nd the approximate solution yn+1 at time in\" using the formulas Ell-n+1 = ya + %U1 + 23:: + 2kg +k4} where kl=f{tmyn} k2=f(tn+%ayn+%) k3=f(tn+%,yn+%) k4=ftin+h1 yn+ksl We continue this iterative loop until we reach our desired endpoint in time t; . Stated in pseudocode: n = 0 to = 0 y (to) = yo WHILE to