Tom?s Inc. makes two salsa products: Western Foods salsa and Mexico City salsa. Essentially, the two products have different blends of whole tomatoes, tomato sauce, and tomato paste. A jar of Western Foods salsa uses 5 ounce of whole tomatoes, 3 ounces of tomato sauce, and 2 ounces of tomato paste. A jar of Mexico City salsa consists of 7 ounces of whole tomatoes, 1 ounce of tomato sauce, and 2 ounces of tomato paste.

For the current production period Tom?s Inc. can purchase up to 4480 ounces of whole tomatoes,

2080 ounces of tomato sauce, and 1600 ounces of tomato paste. Tom?s Inc. makes a profit of $1.00 per jar of Western Foods salsa and $1.25 per jar of Mexico City salsa. The following linear optimization model was used to determine the mix of salsa products that will maximize the total profit contribution.

Let

W be the number of jars of Western Foods Salsa

M be the number of jars of Mexico City Salsa

Maximize 1W + 1.25M

s.t.

5W + 7M ? 4480 (Whole tomatoes)

3W + 1M ? 2080 (Tomato sauce)

2W + 2M ? 1600 (Tomato paste)

W, M ? 0

The problem was solved in Excel and the sensitivity report is shown below. Answer the following questions based on the sensitivity report. (If a question can?t be answered using the sensitivity report say so. You don?t need to change the model and solve it.)

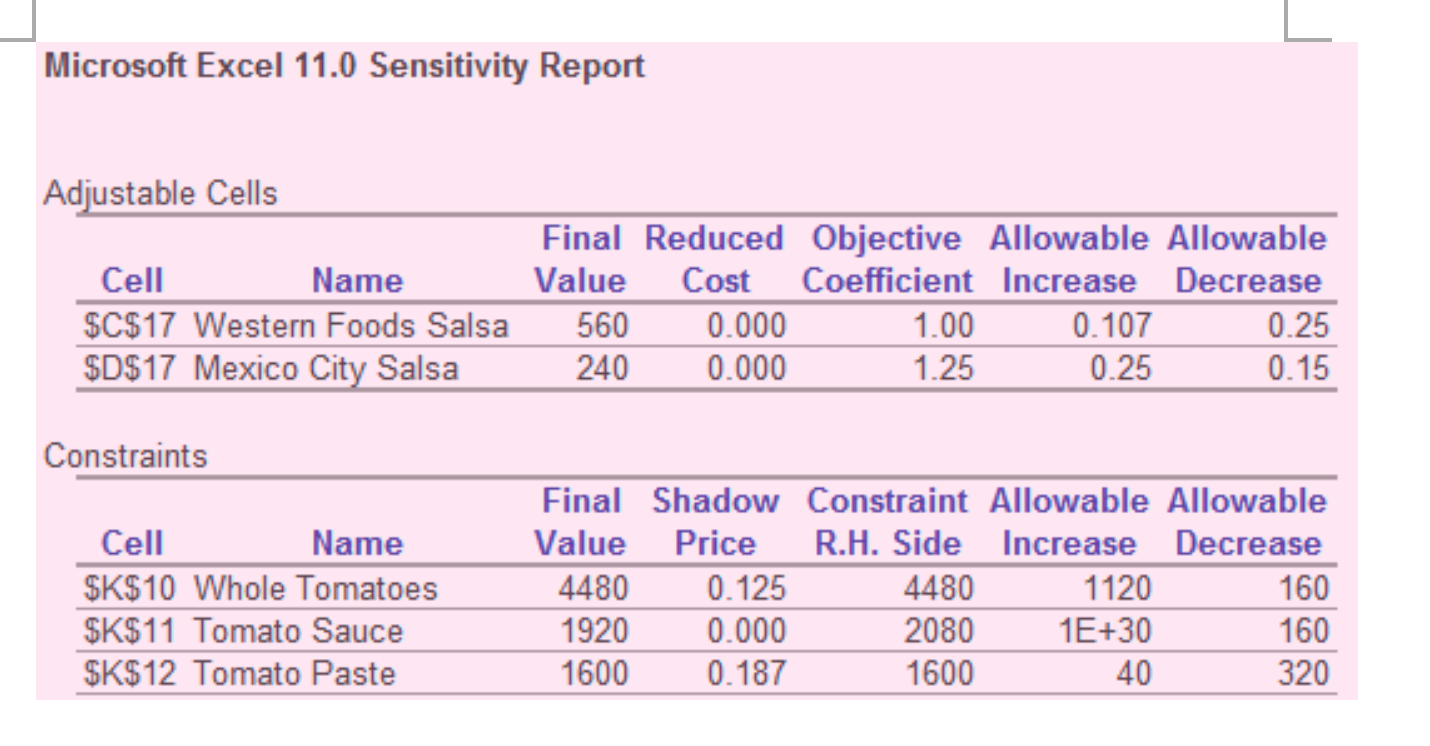
1. What the new total profit (objective value) would be if the profit of a jar of Western Foods salsa changes to $1.2?
2. What would be the value of 30 more ounces of tomato paste? (Refer to the definition of shadow price).
3. How much less profit would Tom?s make if they had 100 fewer ounces of tomato sauce?
4. How would Tom?s profit change if they 500 more ounces of tomato sauce?
5. How would Tom?s profit change if they had 170 more ounces of whole tomatoes?

Microsoft Excel 11.0 Sensitivity Report Adjustable Cells Cell Name $C$17 Western Foods Salsa $D$17 Mexico City Salsa Constraints Cell Name $K$10 Whole Tomatoes $K$11 Tomato Sauce $K$12 Tomato Paste Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 560 240 0.000 0.000 4480 1920 1600 1.00 1.25 0.125 0.000 0.187 Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 0.107 0.25 4480 2080 1600 0.25 0.15 1120 1E+30 40 160 160 320