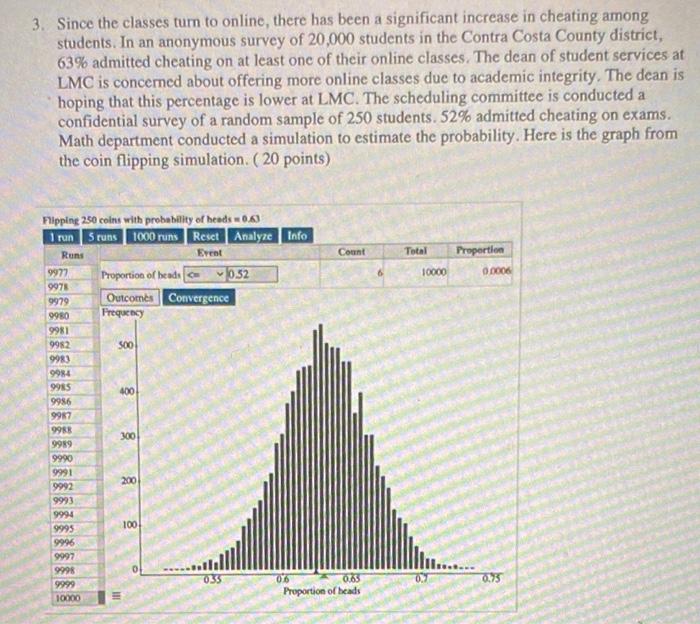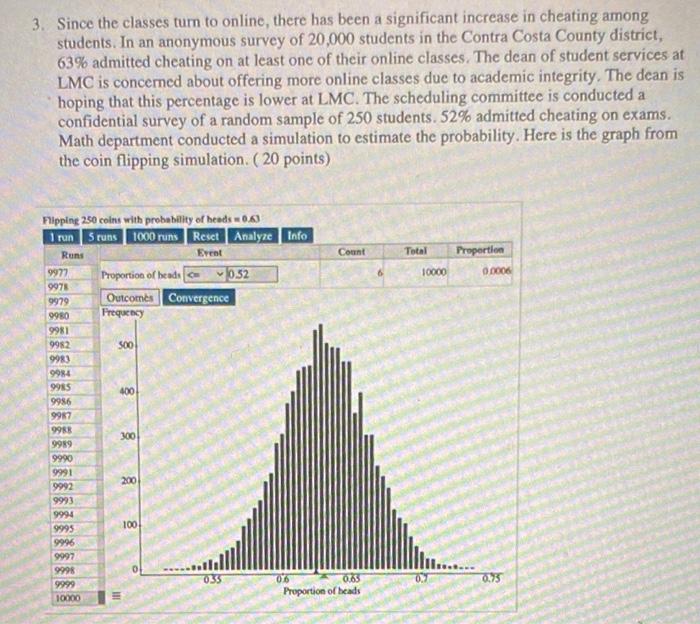
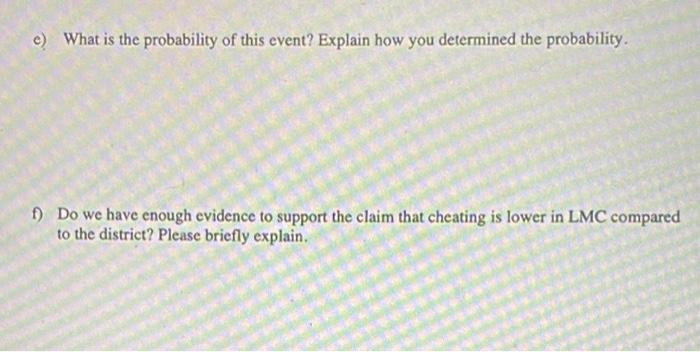
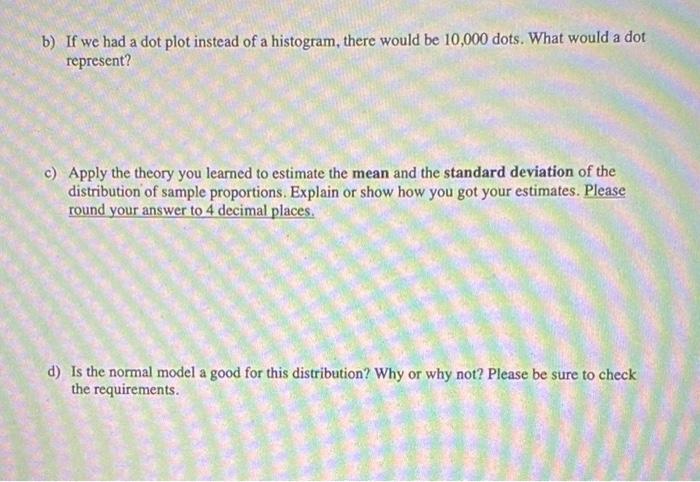
3. Since the classes turn to online, there has been a significant increase in cheating among students. In an anonymous survey of 20,000 students in the Contra Costa County district, 63% admitted cheating on at least one of their online classes. The dean of student services at LMC is concerned about offering more online classes due to academic integrity. The dean is hoping that this percentage is lower at LMC. The scheduling committee is conducted a confidential survey of a random sample of 250 students. 52% admitted cheating on exams. Math department conducted a simulation to estimate the probability. Here is the graph from the coin flipping simulation. (20 points) Flipping 250 coins with probability of heads 0.63 1 run 5 runs 1000 runs Reset Analyze Info Runs Event Total Proportion 0.0006 Proportion of beads 0.52 Outcomes Convergence Frequency 500 400 0.75 9977 9978 9979 9980 9981 9982 9983 9984 9985 9986 9987 9988 9989 9990 9991 9992 9993 9994 9995 9996 9997 9998 9999 10000 300 200 III 100 035 Count 06 0.65 Proportion of heads 10000 0.7 e) What is the probability of this event? Explain how you determined the probability. f) Do we have enough evidence to support the claim that cheating is lower in LMC compared to the district? Please briefly explain. b) If we had a dot plot instead of a histogram, there would be 10,000 dots. What would a dot represent? c) Apply the theory you learned to estimate the mean and the standard deviation of the distribution of sample proportions. Explain or show how you got your estimates. Please round your answer to 4 decimal places. d) Is the normal model a good for this distribution? Why or why not? Please be sure to check the requirements. 3. Since the classes turn to online, there has been a significant increase in cheating among students. In an anonymous survey of 20,000 students in the Contra Costa County district, 63% admitted cheating on at least one of their online classes. The dean of student services at LMC is concerned about offering more online classes due to academic integrity. The dean is hoping that this percentage is lower at LMC. The scheduling committee is conducted a confidential survey of a random sample of 250 students. 52% admitted cheating on exams. Math department conducted a simulation to estimate the probability. Here is the graph from the coin flipping simulation. (20 points) Flipping 250 coins with probability of heads 0.63 1 run 5 runs 1000 runs Reset Analyze Info Runs Event Total Proportion 0.0006 Proportion of beads 0.52 Outcomes Convergence Frequency 500 400 0.75 9977 9978 9979 9980 9981 9982 9983 9984 9985 9986 9987 9988 9989 9990 9991 9992 9993 9994 9995 9996 9997 9998 9999 10000 300 200 III 100 035 Count 06 0.65 Proportion of heads 10000 0.7 e) What is the probability of this event? Explain how you determined the probability. f) Do we have enough evidence to support the claim that cheating is lower in LMC compared to the district? Please briefly explain. b) If we had a dot plot instead of a histogram, there would be 10,000 dots. What would a dot represent? c) Apply the theory you learned to estimate the mean and the standard deviation of the distribution of sample proportions. Explain or show how you got your estimates. Please round your answer to 4 decimal places. d) Is the normal model a good for this distribution? Why or why not? Please be sure to check the requirements