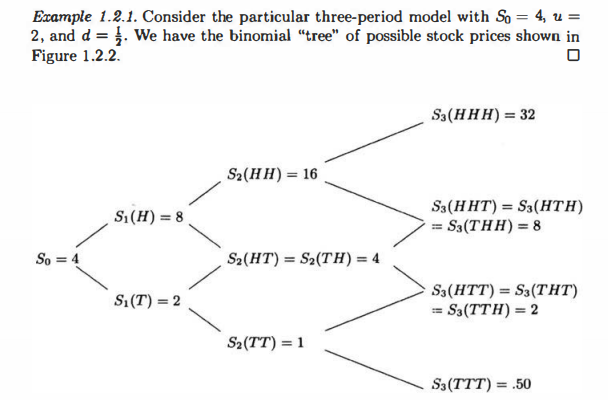
Example 1.2.1. Consider the particular three-period model with So = 4, u = 2, and d = 1. We have the binomial "tree" of possible stock prices shown in Figure 1.2.2. Sz(HHH) = 32 S2(HH) = 16 S (H) = 8 S3(HHT) = S(HTH) S3(THH) = 8 So = 4 S2(HT) = S(TH) = 4 S(T) = 2 Sz(HTT) = S(THT) = S3(TTH) = 2 S2(TT) = 1 S(TTT) = .50 k=0,..., Problem 2. Consider a three-period model of Example 1.2.1 on p. 9 with So = 4, u = 2, d = and interest rate r = = 1, so that = q = }. For n= 0,1, 2, 3, define Mn. max Sk, the maximum of the stock price between times zero and n. Consider a floating strike lookback option, whose payoff at time T = 3 is given by My - St> 0. Let un(s, m) be price of the option at time n if Sn = s and Mn = m. In particular, v3(s, m) = m-s. (i) Develop an algorithm for computing Un recursively. In particular, write a formula for Un in terms of Un+1. (ii) Apply the algorithm developed in (i) to compute vo(4,4). (iii) Provide a formula for on(s, m), the number of shares of stock that should be held by the replicating portfolio at time n if Sn = s and Mn = m. You may assume that the functions un(';'), n = 0,..., 3 are already known. Example 1.2.1. Consider the particular three-period model with So = 4, u = 2, and d = 1. We have the binomial "tree" of possible stock prices shown in Figure 1.2.2. Sz(HHH) = 32 S2(HH) = 16 S (H) = 8 S3(HHT) = S(HTH) S3(THH) = 8 So = 4 S2(HT) = S(TH) = 4 S(T) = 2 Sz(HTT) = S(THT) = S3(TTH) = 2 S2(TT) = 1 S(TTT) = .50 k=0,..., Problem 2. Consider a three-period model of Example 1.2.1 on p. 9 with So = 4, u = 2, d = and interest rate r = = 1, so that = q = }. For n= 0,1, 2, 3, define Mn. max Sk, the maximum of the stock price between times zero and n. Consider a floating strike lookback option, whose payoff at time T = 3 is given by My - St> 0. Let un(s, m) be price of the option at time n if Sn = s and Mn = m. In particular, v3(s, m) = m-s. (i) Develop an algorithm for computing Un recursively. In particular, write a formula for Un in terms of Un+1. (ii) Apply the algorithm developed in (i) to compute vo(4,4). (iii) Provide a formula for on(s, m), the number of shares of stock that should be held by the replicating portfolio at time n if Sn = s and Mn = m. You may assume that the functions un(';'), n = 0,..., 3 are already known