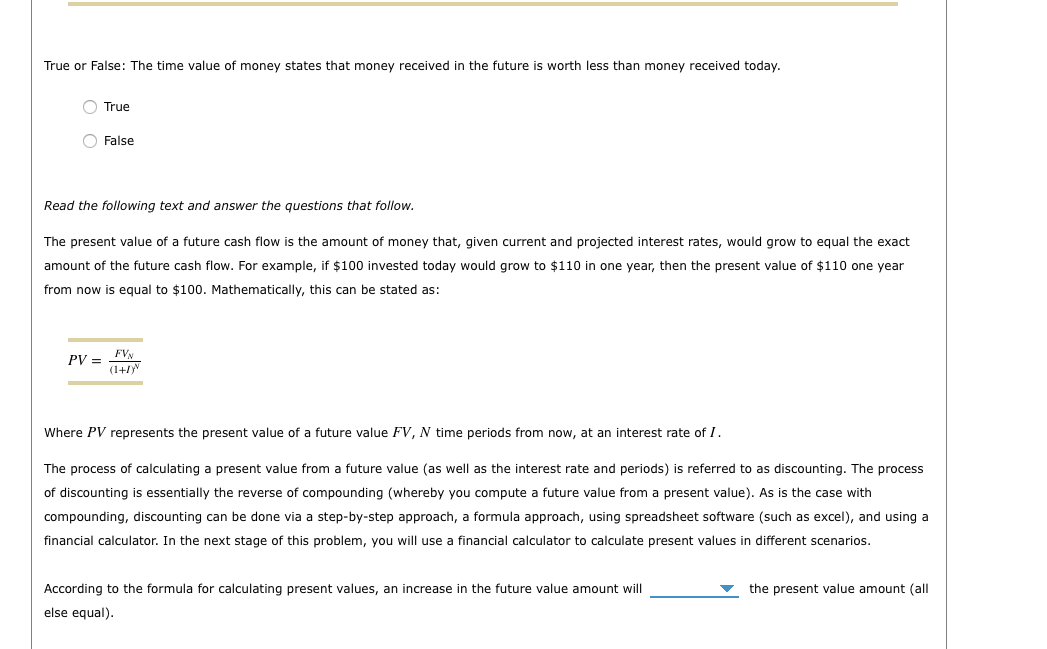
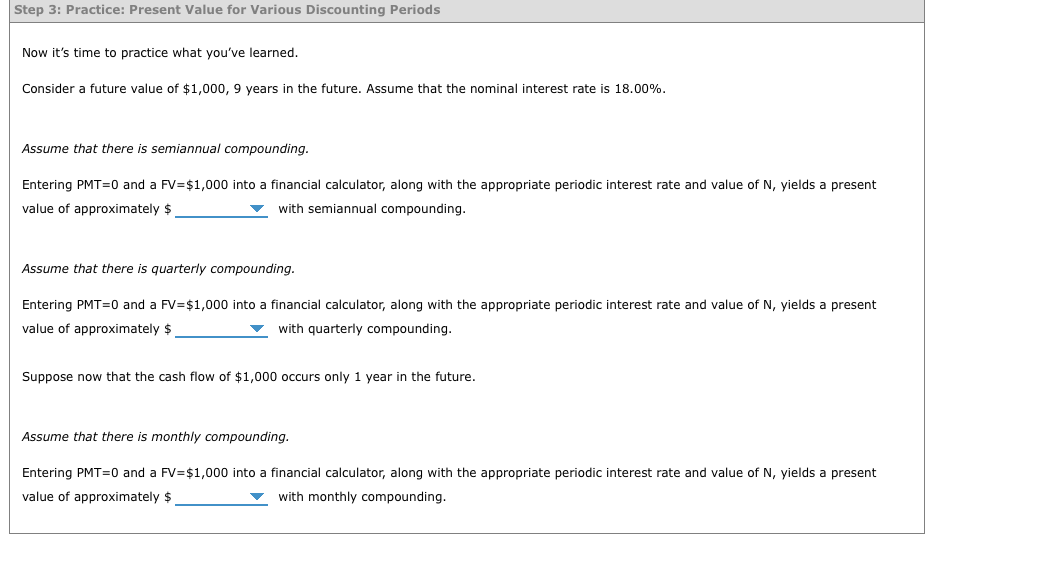
True False Read the following text and answer the questions that follow. amount of the future cash flow. For example, if $100 invested today would grow to $110 in one year, then the present value of $110 one year from now is equal to $100. Mathematically, this can be stated as: PV=(1+I)NFVN Where PV represents the present value of a future value FV,N time periods from now, at an interest rate of of discounting is essentially the reverse of compounding (whereby you compute a future value from a present value). As is the case with compounding, discounting can be done via a step-by-step approach, a formula approach, using spreadsheet software (such as excel), and using a financial calculator. In the next stage of this problem, you will use a financial calculator to calculate present values in different scenarios. According to the formula for calculating present values, an increase in the future value amount will the present value amount (all else equal). Consider a future value of $1,000,8 years in the future. Assume that the nominal interest rate is 9.00%. If you are calculating the present value of this cash flow under semiannual (twice per year) compounding, you would enter for I/Y into your financial calculator. Entering in the values you just calculated for N and I/Y, along with a PMT =0 and a FV=$1,000, into a financial calculator yields a present value of approximately $ with semiannual compounding. If you are calculating the present value of this cash flow under quarterly (four times per year) compounding, your for I/Y into your financial calculator. Entering in the values you just calculated for N and I/Y, along with a PMT =0 and a FV=$1,000, into a financial calculator yields a present value of approximately $ with quarterly compounding. Suppose now that the cash flow of $1,000 only 1 year in the future. If you are calculating the present value of this cash flow under quarterly (12 times per year) compounding, you would enter for I/Y into your financial calculator. Entering in the values you just calculated for N and I/Y, along with a PMT =0 and a FV=$1,000, into a financial calculator yields a present value of approximately $ with monthly compounding. Now it's time to practice what you've learned. Consider a future value of $1,000,9 years in the future. Assume that the nominal interest rate is 18.00%. Assume that there is semiannual compounding. Entering PMT=0 and a FV =$1,000 into a financial calculator, along with the appropriate periodic interest rate and value of N, yields a present value of approximately $ with semiannual compounding. Assume that there is quarterly compounding. Entering PMT=0 and a FV =$1,000 into a financial calculator, along with the appropriate periodic interest rate and value of N, yields a present value of approximately $ with quarterly compounding. Suppose now that the cash flow of $1,000 occurs only 1 year in the future. Assume that there is monthly compounding. Entering PMT=0 and a FV =$1,000 into a financial calculator, along with the appropriate periodic interest rate and value of N, yields a present value of approximately $ with monthly compounding. True False Read the following text and answer the questions that follow. amount of the future cash flow. For example, if $100 invested today would grow to $110 in one year, then the present value of $110 one year from now is equal to $100. Mathematically, this can be stated as: PV=(1+I)NFVN Where PV represents the present value of a future value FV,N time periods from now, at an interest rate of of discounting is essentially the reverse of compounding (whereby you compute a future value from a present value). As is the case with compounding, discounting can be done via a step-by-step approach, a formula approach, using spreadsheet software (such as excel), and using a financial calculator. In the next stage of this problem, you will use a financial calculator to calculate present values in different scenarios. According to the formula for calculating present values, an increase in the future value amount will the present value amount (all else equal). Consider a future value of $1,000,8 years in the future. Assume that the nominal interest rate is 9.00%. If you are calculating the present value of this cash flow under semiannual (twice per year) compounding, you would enter for I/Y into your financial calculator. Entering in the values you just calculated for N and I/Y, along with a PMT =0 and a FV=$1,000, into a financial calculator yields a present value of approximately $ with semiannual compounding. If you are calculating the present value of this cash flow under quarterly (four times per year) compounding, your for I/Y into your financial calculator. Entering in the values you just calculated for N and I/Y, along with a PMT =0 and a FV=$1,000, into a financial calculator yields a present value of approximately $ with quarterly compounding. Suppose now that the cash flow of $1,000 only 1 year in the future. If you are calculating the present value of this cash flow under quarterly (12 times per year) compounding, you would enter for I/Y into your financial calculator. Entering in the values you just calculated for N and I/Y, along with a PMT =0 and a FV=$1,000, into a financial calculator yields a present value of approximately $ with monthly compounding. Now it's time to practice what you've learned. Consider a future value of $1,000,9 years in the future. Assume that the nominal interest rate is 18.00%. Assume that there is semiannual compounding. Entering PMT=0 and a FV =$1,000 into a financial calculator, along with the appropriate periodic interest rate and value of N, yields a present value of approximately $ with semiannual compounding. Assume that there is quarterly compounding. Entering PMT=0 and a FV =$1,000 into a financial calculator, along with the appropriate periodic interest rate and value of N, yields a present value of approximately $ with quarterly compounding. Suppose now that the cash flow of $1,000 occurs only 1 year in the future. Assume that there is monthly compounding. Entering PMT=0 and a FV =$1,000 into a financial calculator, along with the appropriate periodic interest rate and value of N, yields a present value of approximately $ with monthly compounding