Question: Tut Exerc e The position of a particle is given by the expression x = 5.00 cos (5.007rt + 71/4), where x is in meters
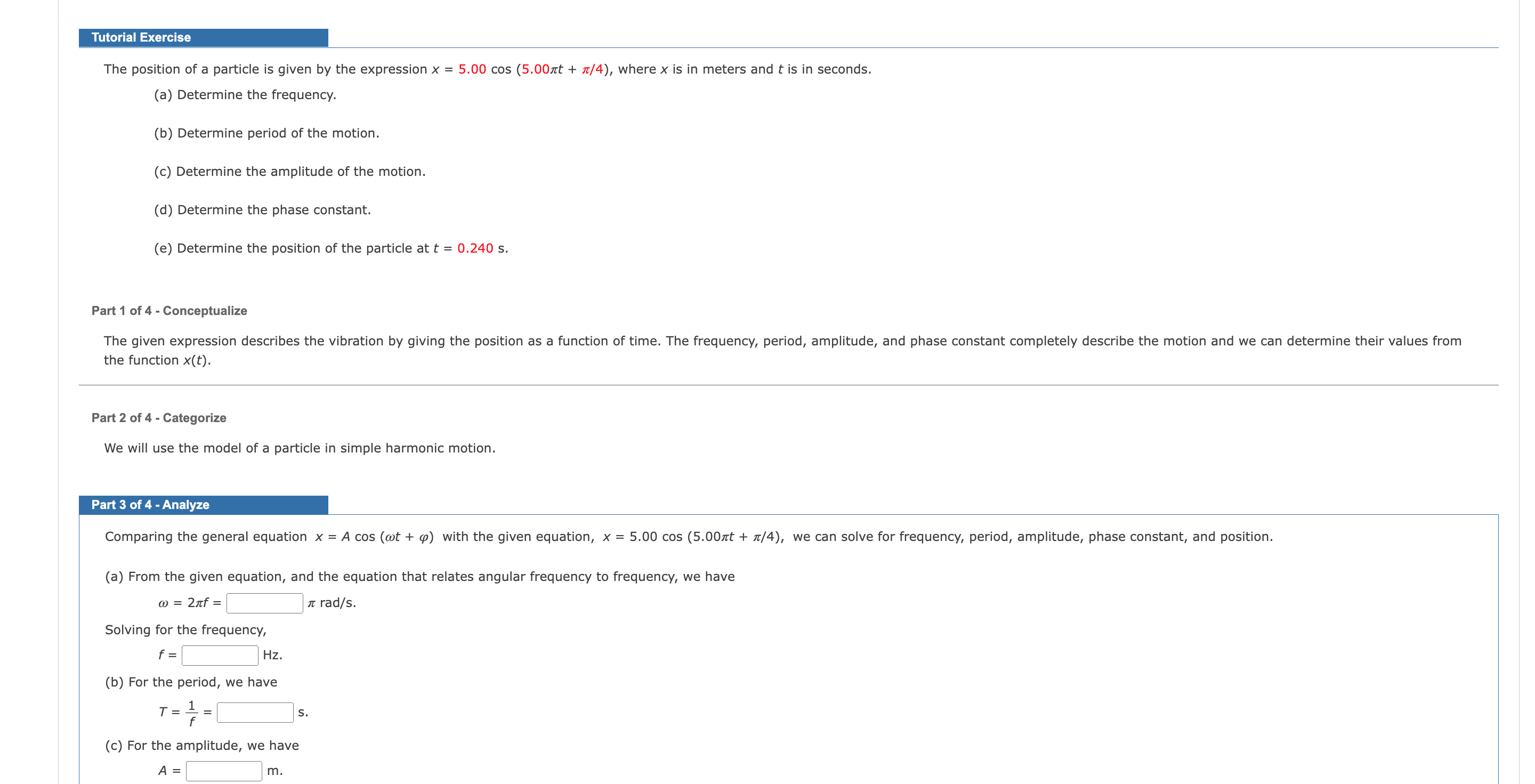
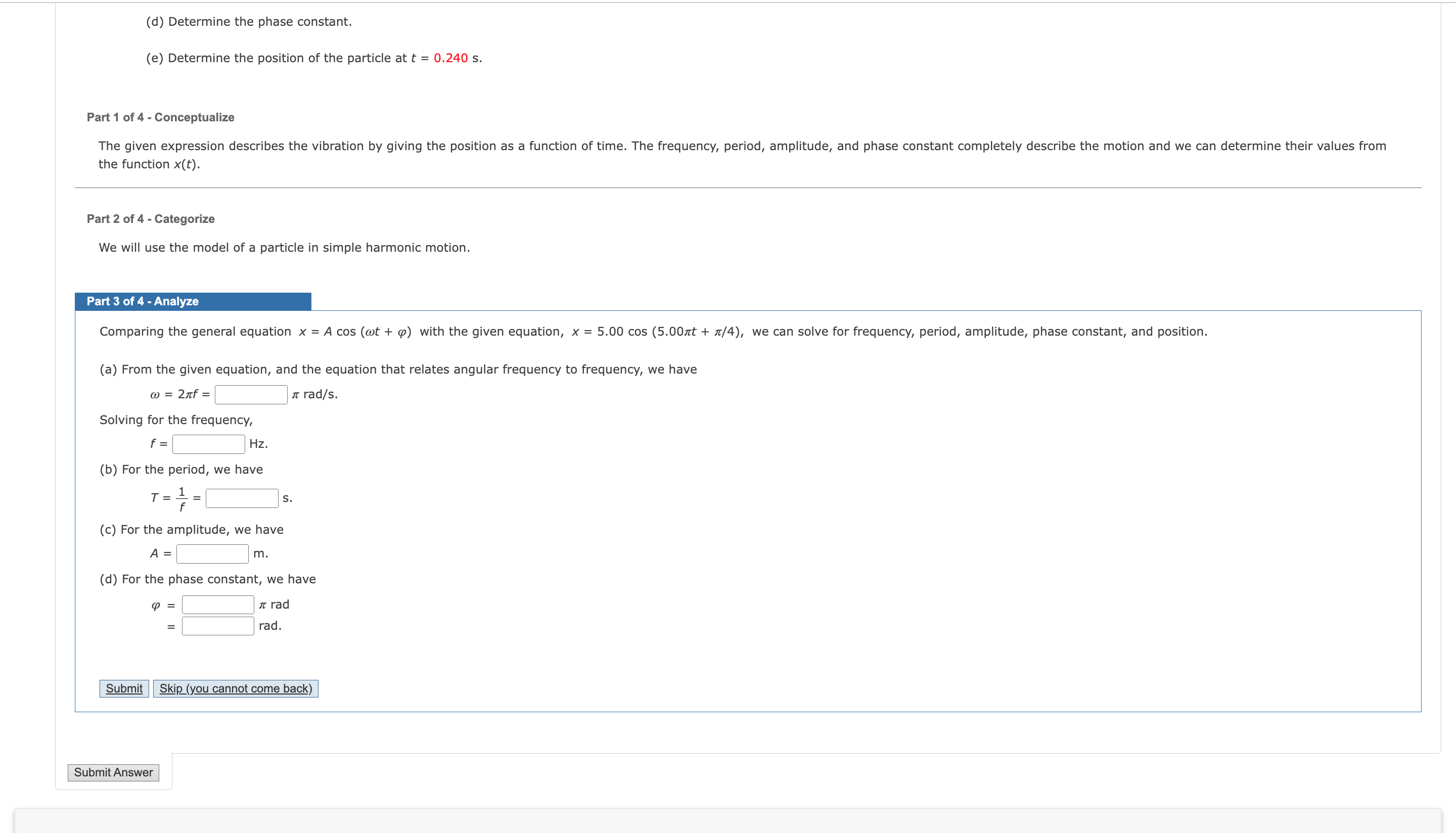
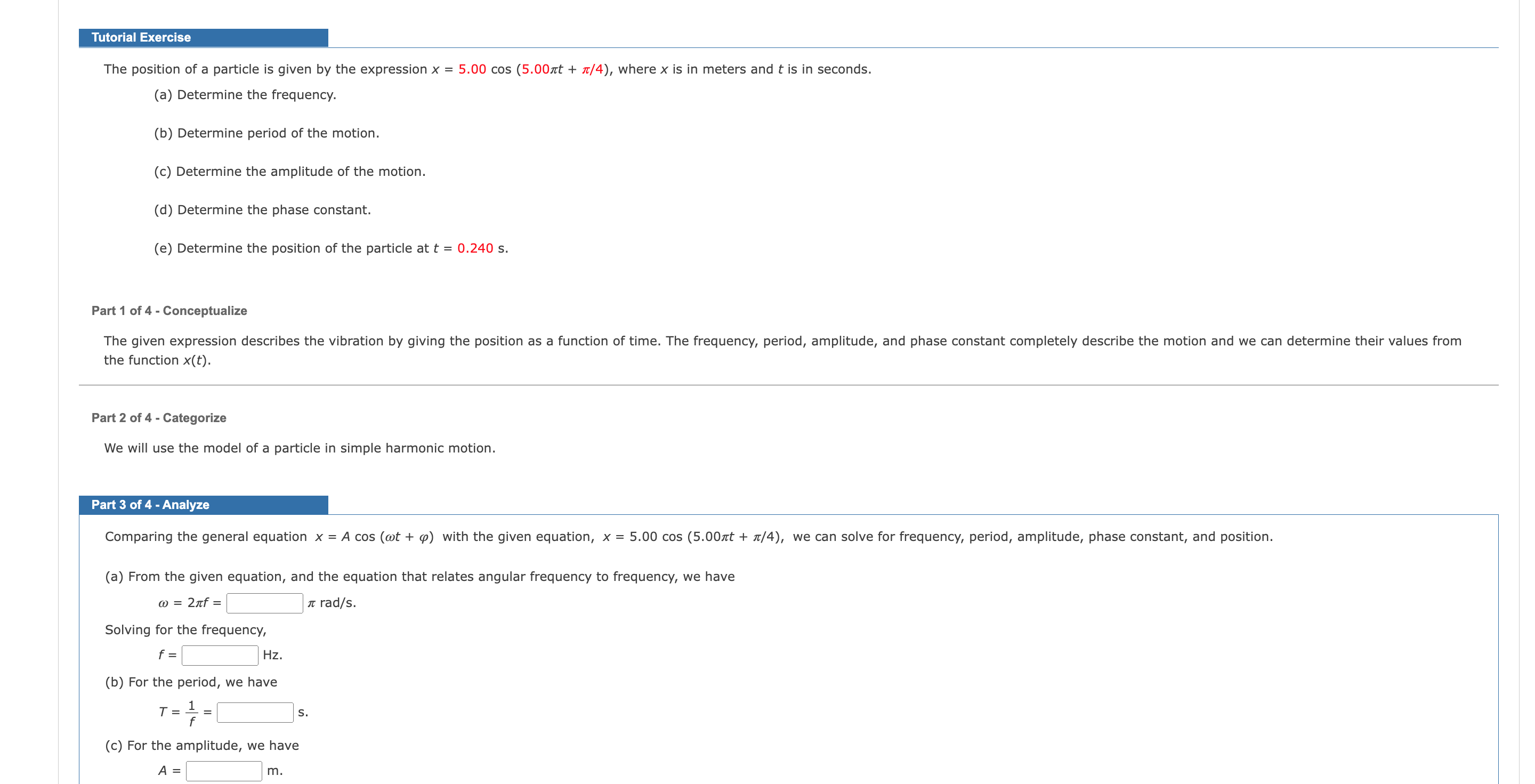
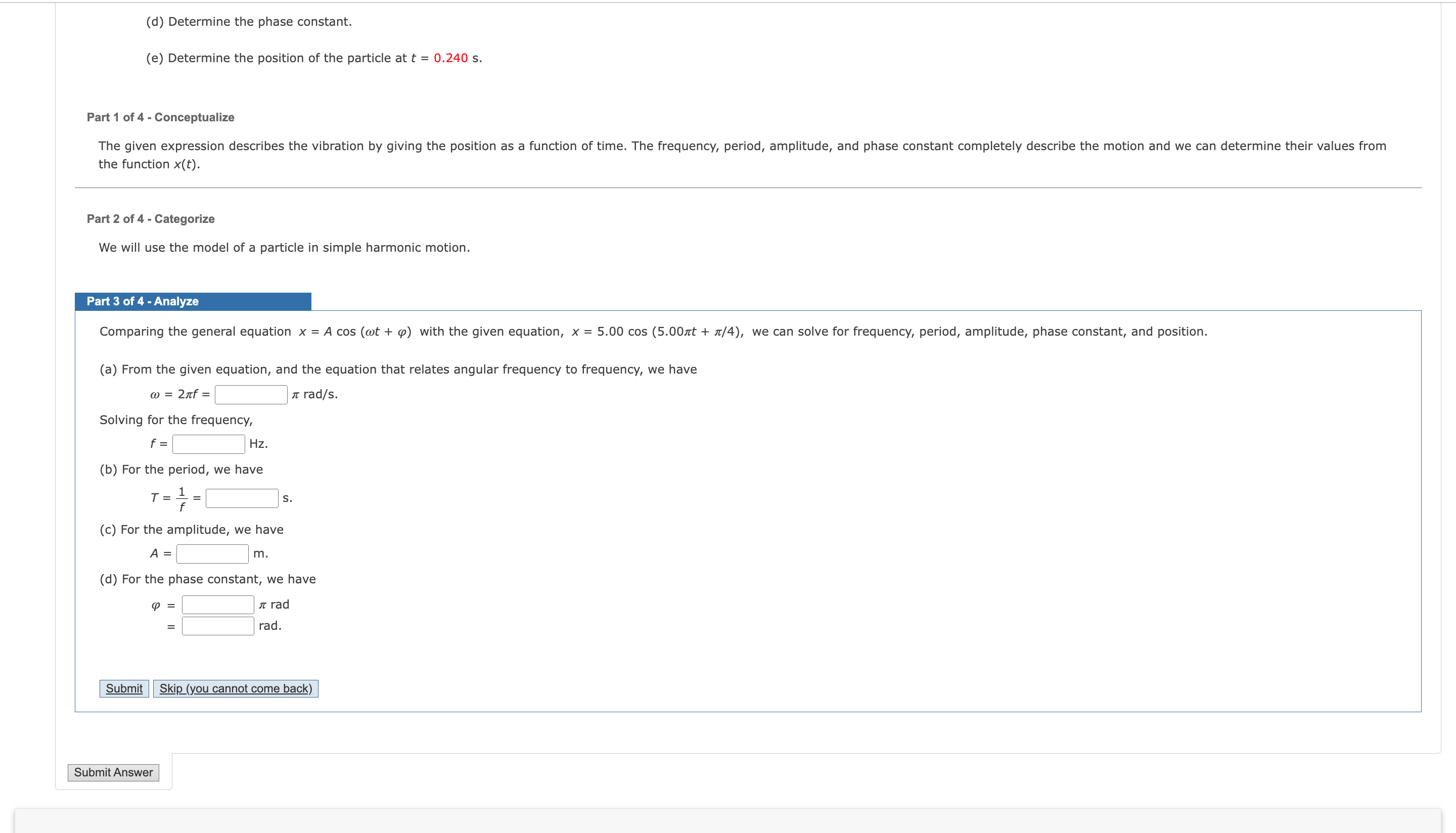
Tut Exerc e The position of a particle is given by the expression x = 5.00 cos (5.007rt + 71/4), where x is in meters and t is in seconds. (a) Determine the frequency. (b) Determine period of the motion. (c) Determine the amplitude of the motion. (d) Determine the phase constant. (e) Determine the position of the particle at t = 0.240 5. Pan 1 of 4 - Conceptualize The given expression describes the vibration by giving the position as a function of time. The frequency, period, amplitude, and phase constant completely describe the motion and we can determine their values from the function x(t). Part 2 of 4 - Categorize We will use the model of a particle in simple harmonic motion. Pan 3 of 4 - Analyze Comparing the general equation x = A cos (wt + (a) with the given equation, x = 5.00 cos (5,00nt + 71/4), we can solve for frequency, period, amplitude, phase constant, and position. (a) From the given equation, and the equation that relates angular frequency to frequency, we have a; = 27rf= 7r rad/s. Solving for the frequency, f: HZ. (b) For the period, we have _ 1 _ 7 :15- (c) For the amplitude, we have A: m. (d) Determine the phase constant. (e) Determine the position of the particle at t = 0.240 s. Pan1 of 4 - Conceptualize The given expression describes the vibration by giving the position as a function of time. The frequency, period, amplitude, and phase constant completely describe the motion and we can determine their values from the function x(t). Pan 2 of 4 - Categorize We will use the model of a particle in simple harmonic motion. Part 3 of 4 - Analyze Comparing the general equation x = A cos (wt + (a) with the given equation, x = 5.00 cos (5.00m + \"/4), we can solve for frequency, period, amplitude, phase constant, and position. (a) From the given equation, and the equation that relates angular frequency to frequency, we have m = 2m': It rad/s. Solving for the frequency, f: Hz. (b) For the period, we have _ 1 _ T 7 s. (c) For the amplitude, we have (d) For the phase constant, we have (a = I: rad = rad. Submit $1.; (you cannot come back) Submit
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


