Two items A and B can be produced in 4 different processes which require different amounts of equipment, labor and raw materials. These resources are limited and the sale of these items generates a known profit depending on the process with which they are made. It is about determining the quantity of items to be produced in each process in order to maximize profit. The required and available resources, as well as the profit generated by each item unit, are shown in the following table:

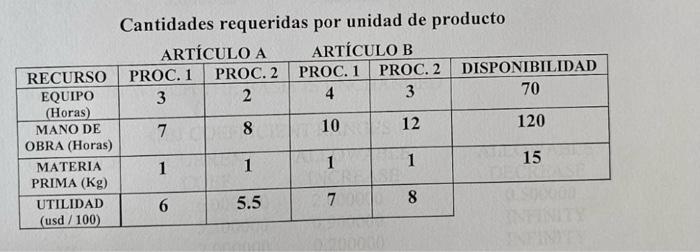
The Linear Programming model is as follows: Maximize 6x1+5.5x2+7y1+8y2 Subject to: 3x1+2x2+4y1+3y2

x1+x2+y1+y2

Below are the results that LINDO (Software for Integer Programming, Linear Programming, Nonlinear Programming, Stochastic Programming, Global Optimization) returns for this problem:

With this information, answer the following questions:

1) What is the optimal production schedule? 2) Within what range of values could the profit of product B change with process 2? What would be the optimal profit when Cj for Y2=9?

3) Suppose that simultaneously the unit gain of X1 and Y2 change from 6 to 8.50 and 8 to 9 respectively. Does the optimal solution change? Yes or No Why?

4) Why is the dual price for the equipment 0?

5) What would be the increase in the objective function for an additional unit of labor?

6) What is the dual price for the raw material?

7) How much is the most the company would be willing to pay for an additional hour of labor?

Cantidades requeridas por unidad de producto OBJECTIVE FUNCTION VALUE 1) 96.00000 NO. ITERATIONS =2 RANGES IN WHICH THE BASIS IS UNCHANGED