Question: Two statements X and Y are logically equivalent if any of the following two conditions hold: 1. The truth tables of each statement have

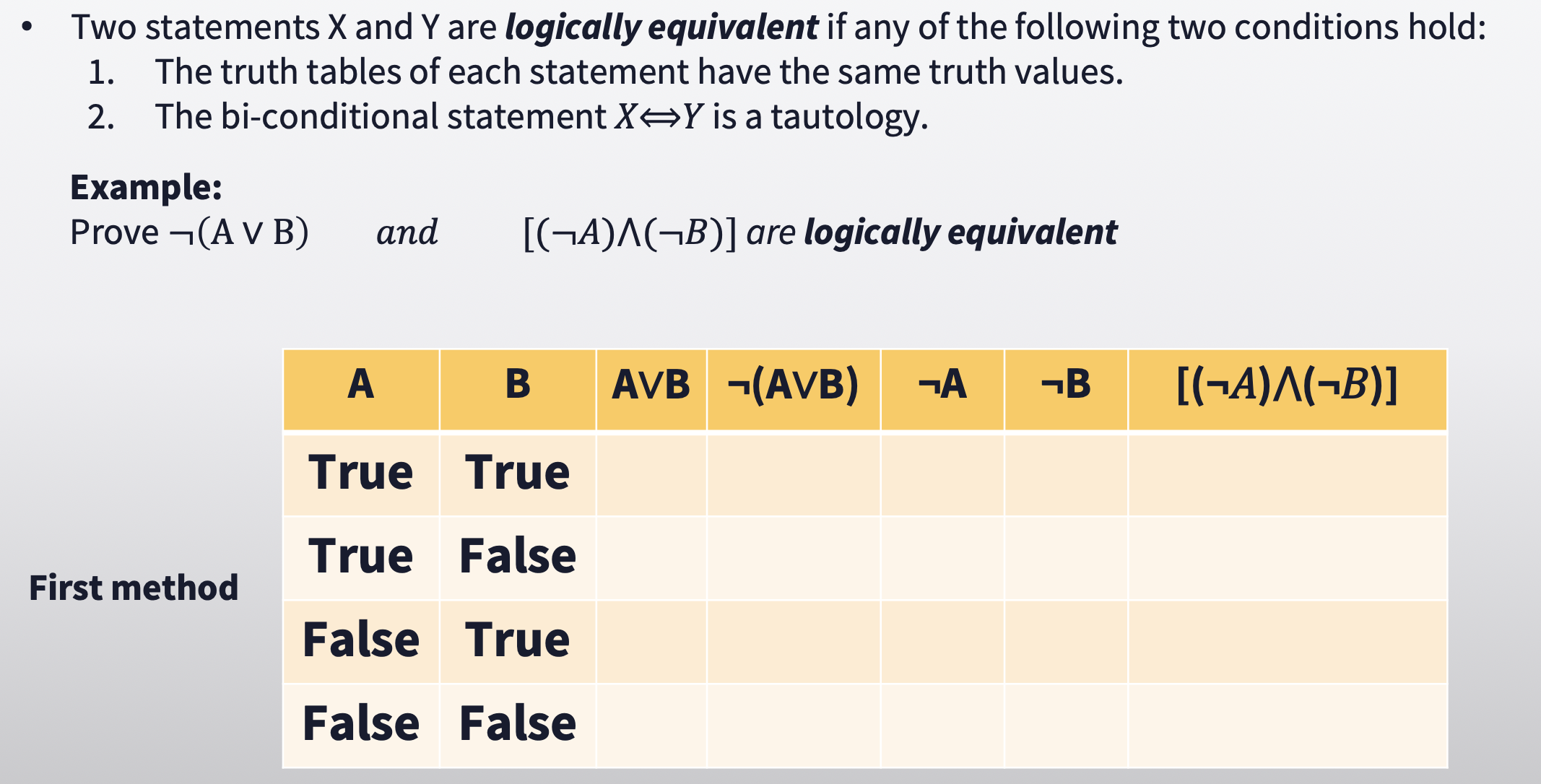
Two statements X and Y are logically equivalent if any of the following two conditions hold: 1. The truth

Two statements X and Y are logically equivalent if any of the following two conditions hold: 1. The truth tables of each statement have the same truth values. 2. The bi-conditional statement XY is a tautology. Example: Prove - (A V B) First method and [(A)^(B)] are logically equivalent B AVB (AVB) A B A True True True False False True False False [(A)^(B)] Two statements X and Y are logically equivalent if any of the following two conditions hold: 1. The truth tables of each statement have the same truth values. 2. The bi-conditional statement X Y is a tautology. Example: Prove (A V B) First method and [(A)^(B)] are logically equivalent B AVB -(AVB) A B A True True True False False True False False [(A)^(B)]

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The question youre asking involves filling out a truth table to show that the statem... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

Write down the uncovered interest rate parity condition. Explain, in your own words, what it means intuitively. (5 points) Suppose we were to run a Fama regression" of the form log S log S = a+ (,...

If x and y are nonzero vectors in Rn and A = xyT, then the row echelon form of A will have exactly one nonzero row. In this case answer true if the statement is always true and false otherwise. In...

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

An experiment was performed to assess the effects of a change in the manufacturing procedure on the average potency of a tablet product. A new batch of antibiotic tablets was made with a modification...

Why number 15 showing problem? Tutorial4.java Tutorial5.java Tutorial3.java *VRecord.java x 2 public class VRecord 3 1 4 public static void main(String[] args) {} 5 public int VID; 6 public String...

Sec. 10.1 Guided Worksheet Submission Activity Guided Practice Activity #1 Conditionally Speaking Contrapositive: If not Q then not P. If not P then not Q. Two statements are said to be logically...

Problem 1: Determine whether or not the following two statements, (a) and (b), are logically equivalent. (You may use truth tables or logical properties but must use some form of formal argument for...

Let the following statements be given p = "You can vote." q = "You are under 18 years old." r = "You are from Mars." Translate the following statement into symbols of formal logic. you can't vote if...

Question 24 1 pts Use the definitions of the variables below to translate each English statement into an equivalent logical expression. y: the applicant is at least eighteen years old p: the...

Need help for a truth table, below are the questions for them. Multiple choice ones 1.) Statements (1) and (2) are logically equivalent. (True/False)? 2.) Which of the following is a correct...

Continental Global Services has been experiencing several problems to deliver projects on time and within budget. After a careful assessment, senior management found out there was not a lack of...

Find the nominal annual rate of interest (a) At which $2500 will grow to $4000 in eight years compounded quarterly; (b) At which money will double in five years if compounded semi-annually; (c) If...

q , 7 . True or False: A problem with Operating Cash Flow is that not all of it is available for distribution to investors - those people / entities that provided the firm with capital when it...

List the major parts of a multi-step corporate income statement for Star Pilates Trainers Inc. for the year ended December 31, 2020. Include all the major parts of the income statement, starting with...

FG specializes in the manufacture of tablets, laptops and desktop PCs. FG currently operates a standard absorption costing system. Budgeted information for next year is given below: Fixed production...

What private sector company epitomizes the concept of a global company with a well managed global supply chain? Provide a rationale for your response.

Given an n-element array X of integers, AlgorithmC executes an O(n)-time computation for each even number in X, and an O(logn)-time computation for each odd number in X. What are the best-case and...

Examine the given control chart for p and determine whether the process is within statistical control. If it is not, identify which of the three out-of-control criteria apply. cens 10 20

Cooperative housingis a unit in a building or complex owned by a nonprofit association or a corporation for the residents use.Group of answer choicesTrueFalse

In Figure 8.7 we decomposed the function f by first identifying sub functions in the columns of the Karnaugh map. Repeat this decomposition by first identifying sub functions in the rows of the...

Write Verilog code for a universal shift register with n bits.

Repeat Problem 9.17 but with the following change in the specification. While w = 1, the output z should have only one pulse; if several pulses occur on c, only the first one should be reproduced on...

What are models and why are they important?

Consider the following four covariance matrices that apply to clusters having four responses per cluster: P Q R S a. Which of the above matrices are heterogeneous (as compared to homogeneous)...

This problem considers the (fictitious) study designed to compare two treatments for the relief of heartburn, described by the data set of Table 25.6. One of two treatments (A = active = 1, P =...