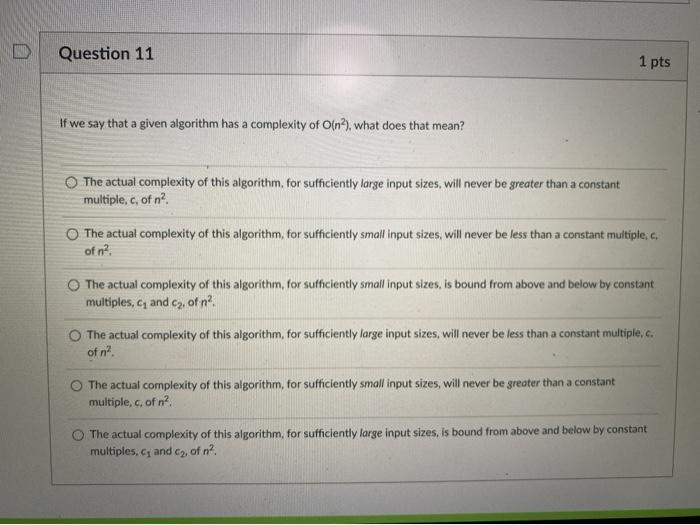
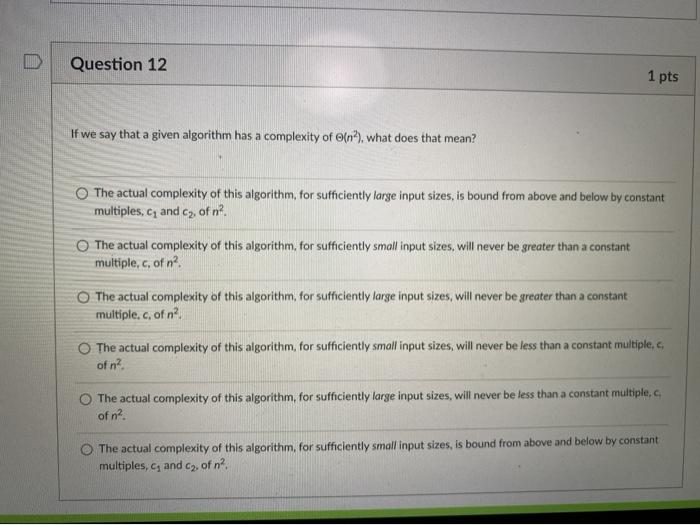
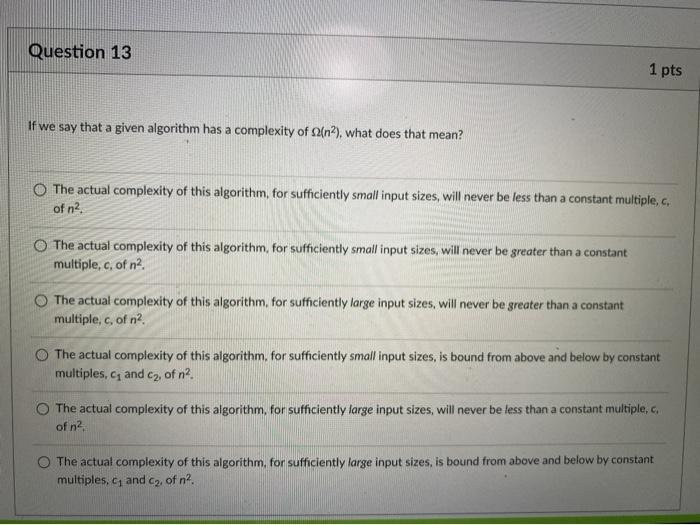
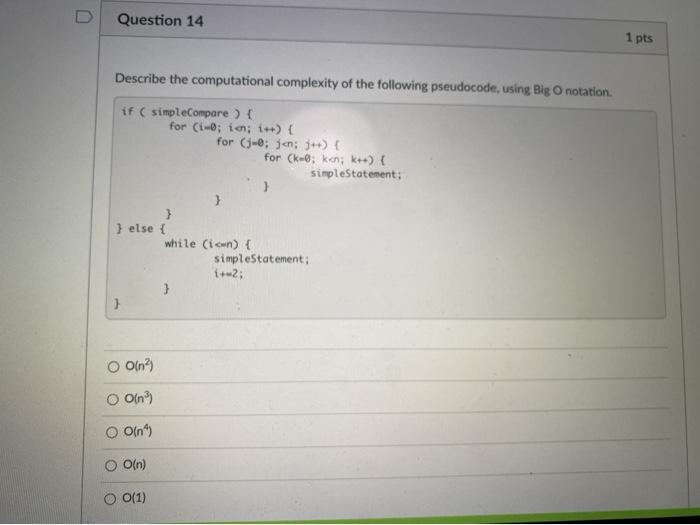
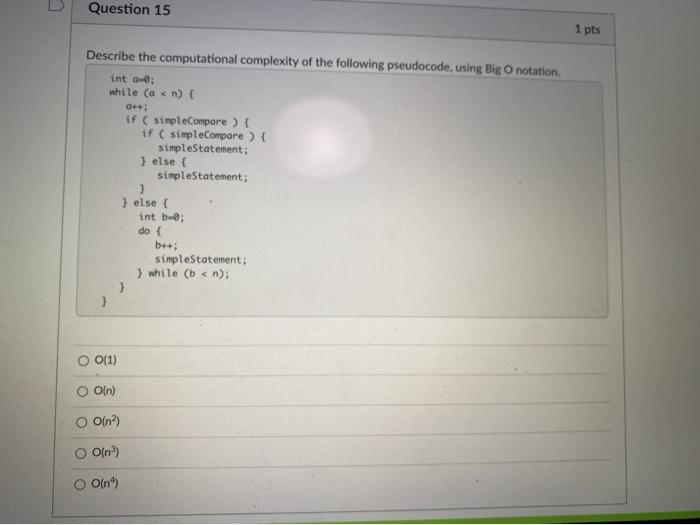
u Question 11 1 pts If we say that a given algorithm has a complexity of O(n), what does that mean? The actual complexity of this algorithm for sufficiently large input sizes, will never be greater than a constant multiple, c, of n? The actual complexity of this algorithm for sufficiently small input sizes, will never be less than a constant multiple of na The actual complexity of this algorithm, for sufficiently small input sizes, is bound from above and below by constant multiples, and cy, of n? The actual complexity of this algorithm for sufficiently large input sizes, will never be less than a constant multiple, c. of n? The actual complexity of this algorithm, for sufficiently small input sizes, will never be greater than a constant multiple, c. of n? The actual complexity of this algorithm, for sufficiently large input sizes, is bound from above and below by constant multiples, and Cz, of n? Question 12 1 pts If we say that a given algorithm has a complexity of efn), what does that mean? The actual complexity of this algorithm, for sufficiently large input sizes, is bound from above and below by constant multiples, C, and cy, of n? The actual complexity of this algorithm, for sufficiently small input sizes, will never be greater than a constant multiple, c, of n? The actual complexity of this algorithm, for sufficiently large input sizes, will never be greater than a constant multiple.c, of n? The actual complexity of this algorithm, for sufficiently small input sizes, will never be less than a constant multiple, of n? The actual complexity of this algorithm, for sufficiently large input sizes, will never be less than a constant multiple, of n? The actual complexity of this algorithm, for sufficiently small input sizes, is bound from above and below by constant multiples, C, and cy, of n? Question 13 1 pts If we say that a given algorithm has a complexity of (n2), what does that mean? The actual complexity of this algorithm, for sufficiently small input sizes, will never be less than a constant multiple, c, of n2 The actual complexity of this algorithm, for sufficiently small input sizes, will never be greater than a constant multiple, c, of na. The actual complexity of this algorithm, for sufficiently large input sizes, will never be greater than a constant multiple, c, of n2 The actual complexity of this algorithm, for sufficiently small input sizes, is bound from above and below by constant multiples, and c2, of n2. The actual complexity of this algorithm, for sufficiently large input sizes, will never be less than a constant multiple, c. of na The actual complexity of this algorithm, for sufficiently large input sizes, is bound from above and below by constant multiples, and C2 of n2. Question 14 1 pts Describe the computational complexity of the following pseudocode, using Big O notation if ( simpleCompare ) for (1-6; im; i--) { for (1-0; j<>