Under certain conditions, we will be building a string one term at a time. It is similar to building a vector one term at a time. The main difference is the statement to create a null string it is done with two single quotes with no space in between:

mantissa = ; 

Whether we start with a null string or not, we will definitely need to concatenate (add) characters (either 1 or 0) onto the string one at a time. The process to do this is the same as for a vector, except that the character being concatenated onto the existing string must be put in single quotes:

mantissa = [mantissa 1]; The MATLAB built-in function dec2bin converts a decimal integer into a binary string.

There are two situations in which you may use it.

1) If the number is 1, we first convert the whole part. You may do this with the dec2bin function.

2) When we normalize the resulting binary number, the exponent is an integer. You may also use dec2bin to convert the exponent integer into a binary string.

I recommend you experiment with the function in the Command Window.

Details

The 32-bit word is of the format presented in class, with 7 bits allotted to the exponent and 23 bits allotted to the mantissa.

Reminders

We are creating a string of 1s and 0s. You are not adding one to anything, you will be concatenating either a character 1 or a character 0 onto an existing string.

Tasks

Task #1 Craft linear pseudo-code for specific inputs

Craft linear pseudo-code that identifies and stores the 32-bit word representation of decimal 14.4. Craft separate linear pseudo-code for decimal -0.01.

Task #2 Convert Task #1 output into pseudo-linear pseudo-code

The pseudo-code from Task #1 is purely linear. It contains simply a list of instructions that should be executed one by one. Our first step in converting this to code is to convert it into pseudo-linear pseudo-code. This is done by introducing decision points in the form of questions and answers. These questions and answers will be critical for Task #3.

Task #3 Convert pseudo-linear code into code

Scour the pseudo-linear code for instances of while loops and if statements. What while loops and if statements have in common is that both contain a logical condition expression. If you remember from Week #1, we said that a logical condition expression can be thought of as asking a question. Each question you inserted in Task #2 represents either awhile loop header or an if statement. A while loop question is asked once at the top of each iteration of the while loop, so it will appear multiple times within the pseudo-linear pseudo-code. However, an if statement could appear inside a loop, so its question could also appear multiple times in the pseudo-linear pseudo-code. So, if you see the same question asked over and over again, how do you determine if it is a while loop header or an if statement within a loop? This way: the answer to an if statement within a loop can go from yes to no and back again as many times as you ask it. In the case of a while loop header question, if yes means that we run the loop (it depends on how we ask the question), then once we encounter a no we stop running the loop (and presumably do something different). (Of course, if no means that we run the loop, then once we encounter a yes we stop running the loop).

Another wrinkle to this task is to get your while loop header expression correct. We often think of the while loop header question in terms of what condition makes us stop the loop (repeat this loop until some condition happens). However, the while loop header expression is in terms of what condition causes the loop to continue running (perform this loop so long as this condition is true).

What I currently have

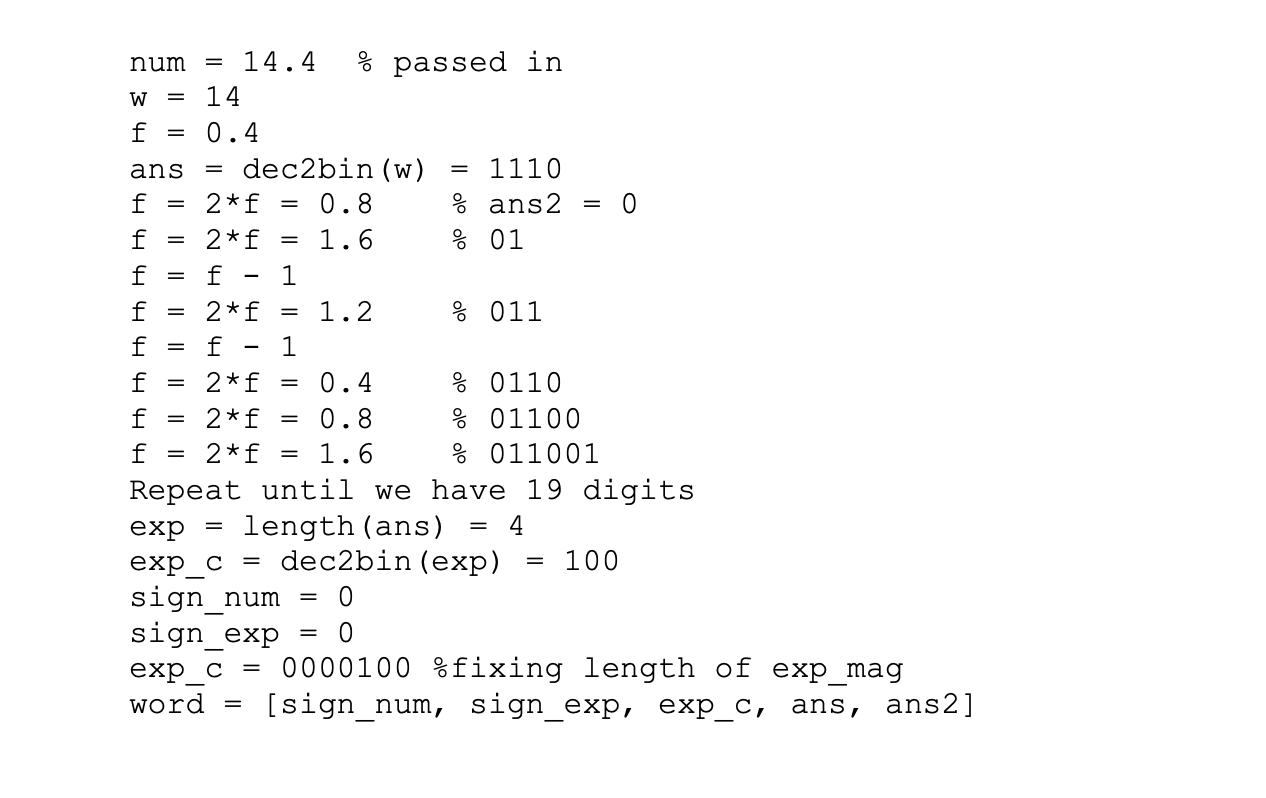
Turn all of this into MATLAB coding

W = = = = = = 0 = = mm H H H H E B th. = = = == num = 14.4 % passed in 14 f 0.4 ans dec2bin (w) 1110 f 2*f 0.8 % ans 2 0 f 2*f 1.6 01 f f 1 f 2*f 1.2 011. f f 1 f 2*f 0.4 % 0110 f 2*f 0.8 % 01100 f = 2*f = 1.6 % 011001 Repeat until we have 19 digits exp length (ans) exp_c = dec2bin (exp) 100 sign_num 0 sign_exp 0 exp_c 0000100 %fixing length of exp_mag word [sign_num, sign_exp, exp_c, ans, ans2] = = = = - = - = = = = UAWNA = = DO = ) + + + + + + + + + + . num -0.01 sign num 1 f = 0.01 %remove sign f = 2* f = 0.02 % exp_mag 1 f = 2* f = 0.04 % exp_mag 2 f = 2*f 0.08 % exp_mag f = 2*f = 0.16 % exp_mag f = 2*f = 0.32 % exp_mag 5 f 2*f = 0.64 % exp_mag 6 f = 2*f = 1.28 % ans 2 1 f f - 1 = 0.28 f = 2*f 0.56 % ans 2 10 f = 2*f 1.12 % ans2 101 f = f - 1 = 0.24 f = 2* f = 0.48 % ans 2 = 1010 f 2*f 0.96 % ans 2 = 10100 f 2*f = 1.92 % ans2 = 101001 f f 1 = 0.92 f = 2*f = 1.84 % ans 2 = 1010011 f f 1 = 0.84 f = 2*f = 1.68 % ans2 = 10100111 f f 1 = 0.68 f 2*f = 1.36 % ans 2 = 101001111 f = f - 1 = 0.36 Repeat until length (ans2) = 23 exp_c = dec2bin (exp_mag) = 110 exp_c 0000110 % zero padding sign_exp = 1 word [sign_num, sign_exp, exp_c, ans2] = = - = - == = = W = is num > 0 Yes: sign_num = 0 No: sign_num 1 num = abs (num) is num 0 Yes: mant = dec2bin (w) deal with f store each and every digit No: mant is length (mant) > 23 Yes: STOP No: f = f*2 is f >= 1 Yes: f = f - 1 mant = [mant, '1'] No: is mant = Yes: exp_mag exp_mag + 1 Nah: mant = [mant, '0'] = deal with f ignore all leading zeros