Under what conditions is (4.9) a convex constraint on x ? Derive (4.14). Define u in (4.14) as u( ) = c2

Under what conditions is (4.9) a convex constraint on ˆx ?

Derive (4.14).

Define u in (4.14) as u(ξ ) = cσ2 −  ξ − u+t 2 2 , where it is known, however, that ξ ≤ U = βa , a.s., for some finite β . For given β and a , can you find c such that (4.14) gives a better bound with this u than with the u used to obtain (4.3)?

Suppose ξi , i = 1,2,3 , are jointly multivariate normally distributed with zero means and variance-covariance matrix

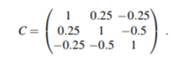
Use Theorem 4 to bound P{ξ ≤ 1 , i = 1,2,3} . What is the exact result? (Hint: Try a transformation to independent normal random variables.)

1 C= 0.25 0.25 -0.25) -0.5 1 -0.25 -0.5 1