UNIT FINAL EXERCISE

4.2 Part 2: Calculating Prime Numbers Write a C program that will ask the user for two natural numbers n1 and n2, and then, using a function compute and (optionally) display all the prime numbers between (and possibly including) n1 and n2. The function will also count and return how many prime numbers exist between n1 and n2. 4.2.1 Finding Prime Numbers A prime is a natural number that is evenly divisible (i.e., no remainder) only by 1 and itself. Here are some ideas, given by a previous class, to help you with developing the algorithms: Ask the user for two positive natural numbers (both >1 by definition) and store the smaller number in a variable named n1 and the larger in a variable named n2. You will need to cycle through all the numbers from n1 to n2 to check if they are prime. Use a variable named p as the loop variable. p=2 is prime by definition. p is prime if it yields all non-zero remainders for the division p/d, for all integers d from 2 to p-1. For example, p=7 is prime because divisions by d=2,3,4,5,6 all have non-zero remainders. An efficient algorithm will stop at the first value of d that determines p is not prime. With p=15, for example, d=3 yields a zero remainder for p/d, so there is no need to test d=4,5,6,,14. Even numbers except 2 are NOT prime. A further gain in efficiency comes when you realize that you only need to check values of d up to the integers just larger or equal to p (let us call this maximum value dMax). Why is that? Well, if p is not prime, then there must be some integer e where p=d*e, and e must be 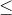dMax. If we started checking from d=2, we would have already found that p/e gave a zero remainder. For example, p=15 yields 15 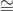3.87, therefore dMax =4. If we tried d=5, we can see that 15/5 gives zero remainder, but so does 15/3 and we would have already tested d=3. Beautiful.

4.2.2 Requirements 1. You must use a program definition and pseudo code (top down design methods) to develop this algorithm 2. Your function must at least find all the prime numbers between n1 and n2 and exploit the p efficiency gain for full marks. 3. You function must ensure n2 is >= n1. If n2 = n1 then the function simply validates if n1 is a prime number. If n1 > n2 then the program will assume an error and swap n1 and n2 and start calculating. 4. You must ask the user if they want to print the prime numbers calculated to the console in a single column, left justified. 5. If the user does not want to print the prime numbers then the program will simply display how many prime numbers exist between n1 and n2. 6. When displaying prime numbers, after the last prime number is displayed the program should display how many prime numbers exist between n1 and n2. For example if the user wants to calculate the prime numbers between 2 and 10, the following would show up on the console.

Enter two natural numbers greater than or equal to 2 separated with commas: 2,10 Display results (y or n): y 2 3 5 7 4 Prime Numbers exist between 2 and 10.

Transcribed image text