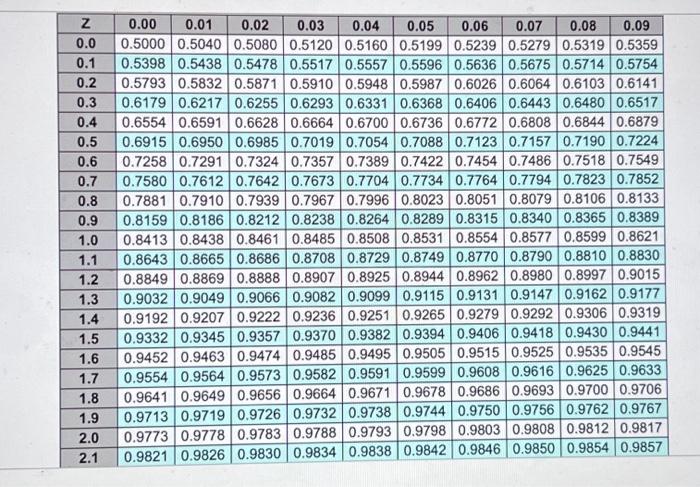
University of Florida football programs are printed 1 week prior to each home game. Attendance averages 75,000 screaming and loyal Gators fans, of whom two-thirds usually buy the program, following a normal distribution, for \\( \\$ 5 \\) each. Unsold programs are sent to a recycling center that pays only 10 cents per program. The standard deviation is 10,000 programs, and the cost to print each program is \\( \\$ 2 \\). Refer to the standard normal table for \\( z \\)-values. a) What is the cost of underestimating demand for each program? \\( \\mathrm{C}_{\\mathrm{s}}=\\$ 3 \\) (round your response to two decimal places). b) What is the overage cost per program? \\[ \\mathrm{C}_{0}=\\$ \\quad \\text { (round your response to two decimal places). } \\] c) How many programs should be ordered per game? programs should be ordered per game (round your response to the nearest whole number). \\begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|} \\hline \\( \\mathbf{Z} \\) & \\( \\mathbf{0 . 0 0} \\) & \\( \\mathbf{0 . 0 1} \\) & \\( \\mathbf{0 . 0 2} \\) & \\( \\mathbf{0 . 0 3} \\) & \\( \\mathbf{0 . 0 4} \\) & \\( \\mathbf{0 . 0 5} \\) & \\( \\mathbf{0 . 0 6} \\) & \\( \\mathbf{0 . 0 7} \\) & \\( \\mathbf{0 . 0 8} \\) & \\( \\mathbf{0 . 0 9} \\) \\\\ \\hline \\( \\mathbf{0 . 0} \\) & 0.5000 & 0.5040 & 0.5080 & 0.5120 & 0.5160 & 0.5199 & 0.5239 & 0.5279 & 0.5319 & 0.5359 \\\\ \\hline \\( \\mathbf{0 . 1} \\) & 0.5398 & 0.5438 & 0.5478 & 0.5517 & 0.5557 & 0.5596 & 0.5636 & 0.5675 & 0.5714 & 0.5754 \\\\ \\hline \\( \\mathbf{0 . 2} \\) & 0.5793 & 0.5832 & 0.5871 & 0.5910 & 0.5948 & 0.5987 & 0.6026 & 0.6064 & 0.6103 & 0.6141 \\\\ \\hline \\( \\mathbf{0 . 3} \\) & 0.6179 & 0.6217 & 0.6255 & 0.6293 & 0.6331 & 0.6368 & 0.6406 & 0.6443 & 0.6480 & 0.6517 \\\\ \\hline \\( \\mathbf{0 . 4} \\) & 0.6554 & 0.6591 & 0.6628 & 0.6664 & 0.6700 & 0.6736 & 0.6772 & 0.6808 & 0.6844 & 0.6879 \\\\ \\hline \\( \\mathbf{0 . 5} \\) & 0.6915 & 0.6950 & 0.6985 & 0.7019 & 0.7054 & 0.7088 & 0.7123 & 0.7157 & 0.7190 & 0.7224 \\\\ \\hline \\( \\mathbf{0 . 6} \\) & 0.7258 & 0.7291 & 0.7324 & 0.7357 & 0.7389 & 0.7422 & 0.7454 & 0.7486 & 0.7518 & 0.7549 \\\\ \\hline \\( \\mathbf{0 . 7} \\) & 0.7580 & 0.7612 & 0.7642 & 0.7673 & 0.7704 & 0.7734 & 0.7764 & 0.7794 & 0.7823 & 0.7852 \\\\ \\hline \\( \\mathbf{0 . 8} \\) & 0.7881 & 0.7910 & 0.7939 & 0.7967 & 0.7996 & 0.8023 & 0.8051 & 0.8079 & 0.8106 & 0.8133 \\\\ \\hline \\( \\mathbf{0 . 9} \\) & 0.8159 & 0.8186 & 0.8212 & 0.8238 & 0.8264 & 0.8289 & 0.8315 & 0.8340 & 0.8365 & 0.8389 \\\\ \\hline \\( \\mathbf{1 . 0} \\) & 0.8413 & 0.8438 & 0.8461 & 0.8485 & 0.8508 & 0.8531 & 0.8554 & 0.8577 & 0.8599 & 0.8621 \\\\ \\hline \\( \\mathbf{1 . 1} \\) & 0.8643 & 0.8665 & 0.8686 & 0.8708 & 0.8729 & 0.8749 & 0.8770 & 0.8790 & 0.8810 & 0.8830 \\\\ \\hline \\( \\mathbf{1 . 2} \\) & 0.8849 & 0.8869 & 0.8888 & 0.8907 & 0.8925 & 0.8944 & 0.8962 & 0.8980 & 0.8997 & 0.9015 \\\\ \\hline \\( \\mathbf{1 . 3} \\) & 0.9032 & 0.9049 & 0.9066 & 0.9082 & 0.9099 & 0.9115 & 0.9131 & 0.9147 & 0.9162 & 0.9177 \\\\ \\hline \\( \\mathbf{1 . 4} \\) & 0.9192 & 0.9207 & 0.9222 & 0.9236 & 0.9251 & 0.9265 & 0.9279 & 0.9292 & 0.9306 & 0.9319 \\\\ \\hline \\( \\mathbf{1 . 5} \\) & 0.9332 & 0.9345 & 0.9357 & 0.9370 & 0.9382 & 0.9394 & 0.9406 & 0.9418 & 0.9430 & 0.9441 \\\\ \\hline \\( \\mathbf{1 . 6} \\) & 0.9452 & 0.9463 & 0.9474 & 0.9485 & 0.9495 & 0.9505 & 0.9515 & 0.9525 & 0.9535 & 0.9545 \\\\ \\hline \\( \\mathbf{1 . 7} \\) & 0.9554 & 0.9564 & 0.9573 & 0.9582 & 0.9591 & 0.9599 & 0.9608 & 0.9616 & 0.9625 & 0.9633 \\\\ \\hline \\( \\mathbf{1 . 8} \\) & 0.9641 & 0.9649 & 0.9656 & 0.9664 & 0.9671 & 0.9678 & 0.9686 & 0.9693 & 0.9700 & 0.9706 \\\\ \\hline \\( \\mathbf{1 . 9} \\) & 0.9713 & 0.9719 & 0.9726 & 0.9732 & 0.9738 & 0.9744 & 0.9750 & 0.9756 & 0.9762 & 0.9767 \\\\ \\hline \\( \\mathbf{2 . 0} \\) & 0.9773 & 0.9778 & 0.9783 & 0.9788 & 0.9793 & 0.9798 & 0.9803 & 0.9808 & 0.9812 & 0.9817 \\\\ \\hline \\( \\mathbf{2 . 1} \\) & 0.9821 & 0.9826 & 0.9830 & 0.9834 & 0.9838 & 0.9842 & 0.9846 & 0.9850 & 0.9854 & 0.9857 \\\\ \\hline \\end{tabular}