Upload all of the code needed to review and test your code along with a sample output that shows that it works. Modify the Red-Black Binary Search Tree as follows: Start with the attached code that will save you a great deal of typing. You must write all of the other code yourself. But, like all code that you get from others, there could be a couple of bugs in the attachment it so make sure that you understand it.

1. Create a toString() method for Node that returns a String representation of the Node's key concatenated with the letter r if it is a red node and concatenated with a space if it is a black node. For example, toString() called on a red node containing the letter 'A' would return "Ar" and for a black node containing the letter 'X' it would return "X "

2. Create a method called toArray() that creates an array of representation of the tree (as opposed to a linked structure with pointers to the left and right children). Because Java is obnoxious with arrays of generics, instead of storing the nodes in the array, store a string representation of the node's key using the toString() method you just wrote.Create a method called printTree that prints the tree showing the hierarchical structure level by level using the array structure. If you can't do it evenly spaced, don't worry.

Please see the attachment for sample output that is nicely spaced not nicely spaced.

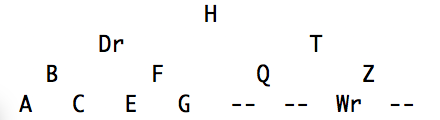
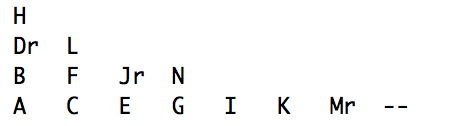
import java.util.Arrays; public class RedBlackBST2, Value> { private static final boolean RED = true; private static final boolean BLACK = false; private Node root; class Node { Key key; Value val; Node left; Node right; int n; boolean colour; Node(Key key, Value val, int n, boolean colour) { this.key = key; this.val = val; this.n = n; this.colour = colour; } } private boolean isRed(Node x) { if (x == null) { return false; } return x.colour == RED; } Node rotateLeft(Node h) { Node x = h.right; h.right = x.left; x.left = h; x.colour = h.colour; h.colour = RED; x.n = h.n; h.n = 1 + size(h.left) + size(h.right); return x; } Node rotateRight(Node h) { Node x = h.left; h.left = x.right; x.right = h; x.colour = h.colour; h.colour = RED; x.n = h.n; h.n = 1 + size(h.left) + size(h.right); return x; } void flipColours(Node h) { h.colour = RED; h.left.colour = BLACK; h.right.colour = BLACK; } private int size(Node x) { return (x==null ? 1 : x.n); } public int size() { return size(root); } public void put(Key key, Value val) { root = put(root, key, val); root.colour = BLACK; } private Node put(Node h, Key key, Value val) { if (h == null) { return new Node(key, val, 1, RED); } int cmp = key.compareTo(h.key); if (cmp  0) { h.right = put(h.right, key, val); } else { h.val = val; } if (isRed(h.right) && !isRed(h.left)) { h = rotateLeft(h); } if (isRed(h.left) && isRed(h.left.left)) { h = rotateRight(h); } if (isRed(h.left) && isRed(h.right)) { flipColours(h); } h.n = size(h.left) + size(h.right); return h; } } 

Dr Dr