Question
Use a systematic approach: Break down the problem into smaller, manageable steps. This will help you stay organized and prevent mistakes. NOTE TUTORS: read the
Use a systematic approach: Break down the problem into smaller, manageable steps. This will help you stay organized and prevent mistakes.
NOTE TUTORS: read the following to help you answer a math question thank you and do entire questions Identify what information is given in the problem and what needs to be found or solved fo. Identify any key words that will guide your thinking when finding a solution. Draw aUse a systematic approach: Break down the problem into smaller, manageable steps. This will help you stay organized and prevent mistakes. diagram or equation if necessary to visualize relationships between numbers or concepts, and organize data points to find solutions. organized plan for solving the problem that involves making assumptions about values when needed and performing calculations where appropriate.. Check your answer against expectations set by the original question before submitting it as your solution! Familiarize yourself with certain strategies such as using inverse operations, using other formulas, working backward from the goal etc., which can help you solve certain types of math problems more easily . Utilize online resources like videos and tutorials to better understand how specific types of math problems are solved in general . Break down large tasks into smaller steps , which can make difficult math problems much easier to tackle . Practice makes perfect - work on solving as many different types of math questions as possible so you can become proficient at them over time ! Ask questions when you need help understanding how a specific type of problem is solved , rather than trying to figure out everything on your own ! Take notes while studying so that you can refer back to them later if needed while working on further challenges Don't be afraid to make mistakes - learn from them so that you don't repeat them next time around! Think outside the box - don't just rely on standard methods for solving every single type of math problem - look for alternate approaches too ! Have patience - learning how to solve difficult maths problems takes time , but with perseverance , anything is possible ! Identify when an equation or expression is missing information and use educated guesses to fill in the gaps.Use a calculator to help with tedious calculations that require many steps of calculation. Work systematically rather than randomly when looking for patterns in data points or equations.. Memorize key formulas and equations so you can quickly access them while solving problems instead of having to look them up every time! Utilize online tools such as graphing calculators, equation solvers, and other interactive resources which can be used to help solve complex math problems more easily . Learn how to use the scientific notation format correctly - it's an important tool that makes calculations involving very large or very small numbers much simpler ! Understand how different operations work together - knowing what happens when you multiply a fraction by an integer , for example , will help you solve certain types of math questions quickly . Simplify your answers as much as possible - this not only helps make sure your solution is correct but also reduces the amount of time needed for future calculations ! . Look out for common mistakes - forgetting negative signs , confusing similar looking symbols etc., can all lead to incorrect solutions if not caught in time ! Keep track of units throughout the problem - make sure all units match up before submitting a final answer! Double check your answers before submitting them- sometimes errors occur during manual calculation that are not easy to spot unless double checked ! Always be aware of any potential implications arising from assumptions made during problem solving - this will help ensure accuracy! Learn how different techniques such as substitution , linear programming , Fourier transforms etc., work so they can be applied appropriately when needed . . If one approach doesn't seem to work, try another approach - there are often multiple ways in which a single problem can be solved successfully .Practice with timed tests and exams regularly so that you don't feel rushed during tests and exams due lack of practice!
Break the problem down into smaller parts: If the problem seems overwhelming, try breaking it down into smaller parts. This can help you identify the key information and steps needed to solve the problem.
Use examples and real-world applications: Try using examples and real-world applications to help you understand the problem. This can make it easier to visualize what is being asked and how to solve it.
Look for patterns and relationships: Try looking for patterns and relationships in the problem. This can help you identify key information and make it easier to solve the problem.
Use estimation: If you are unsure of the exact answer, try using estimation to get a rough idea of what the answer should be. This can help you check your work and make sure you are on the right track.
Check your units: Make sure your units of measurement are consistent throughout the problem. This can help you avoid errors and make it easier to understand your solution.
Simplify your answer: If possible, simplify your answer to make it easier to understand. This can involve reducing fractions, using decimals, or simplifying radical expressions.
Use multiple methods: If you are unsure of the best method to use, try using multiple methods to solve the problem. This can help you check your work and make sure you have found the correct solution.
Ask for help: If you are still having trouble solving the problem, ask for help from a teacher, tutor, or classmate. They may be able to offer insights or tips that can help you understand the problem better.
Stay organized: Keep your work neat and organized to make it easier to follow your thought process. This can also help you avoid mistakes and identify errors.
Review the problem-solving process: After you have solved the problem, take some time to review the problem-solving process. Think about what worked well and what could be improved. This can help you build your math skills and become a more effective problem solver.
Practice mental math: Mental math skills can be very useful when solving math problems. Practice doing basic arithmetic operations in your head to improve your mental math skills.
Use diagrams and graphs: Diagrams and graphs can help you visualize the problem and identify important information. Use them whenever possible to help you understand and solve the problem.
Check for reasonableness: After you have found an answer to the problem, check if it is reasonable. If the answer seems too high or too low, you may have made a mistake or missed a step.
Use logical reasoning: Logical reasoning can be very helpful when solving math problems. Use common sense and logical reasoning to check if your answer makes sense.
Look for shortcuts: Some math problems have shortcuts that can make them easier to solve. Look for patterns and relationships that can help you solve the problem more quickly.
Use technology: There are many tools and resources available to help you solve math problems, including calculators, online resources, and math apps. Use them to help you check your work or solve more complex problems.
Stay calm and focused: Math problems can be challenging, but staying calm and focused can help you stay on track and find the right solution.
Keep a record of your mistakes: Keep a record of the mistakes you make when solving math problems. This can help you identify patterns and areas where you need to improve.
Learn from your mistakes: When you make a mistake, take the time to understand what went wrong and how you can avoid making the same mistake in the future.
Be persistent: Solving math problems can take time and effort, but don't give up. Keep working at it and you will improve your skills and become a more confident problem solver.Use a systematic approach: Break down the problem into smaller, manageable steps. This will help you stay organized and prevent mistakes.

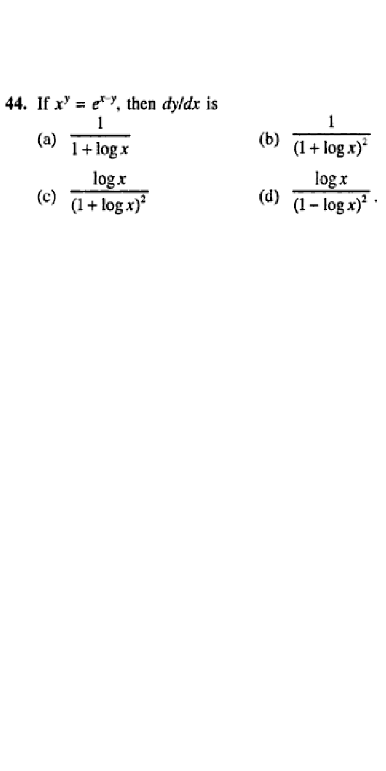
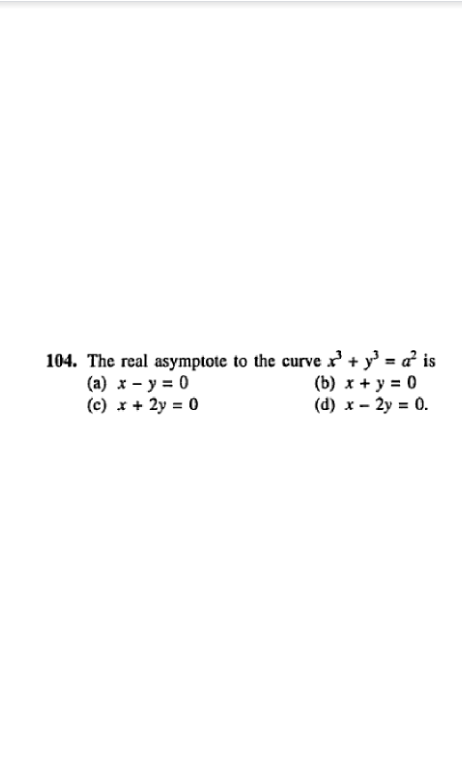









Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


