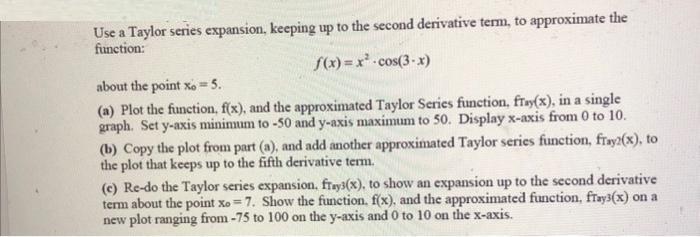
Use a Taylor series expansion, keeping up to the second derivative term, to approximate the function: f(x)=x-cos(3-x) about the point xo = 5. (a) Plot the function, f(x), and the approximated Taylor Series function, fray(x), in a single graph. Set y-axis minimum to -50 and y-axis maximum to 50. Display x-axis from 0 to 10. (b) Copy the plot from part (a), and add another approximated Taylor series function, fray2(x), to the plot that keeps up to the fifth derivative term. (c) Re-do the Taylor series expansion, fray3(x), to show an expansion up to the second derivative term about the point xo=7. Show the function. f(x), and the approximated function, fray3(x) on a new plot ranging from -75 to 100 on the y-axis and 0 to 10 on the x-axis.