Use C++ to code a program that solves a a linear system of equations using Gauss-Seidel, Jacobi, and Successive over relaxation(SOR) methods.

I was able to complete the Gauss/Jacobi methods. However, I am stuck on the SOR method. Below is code that I have thus far. SOR method is needed for case 3. Please help.

Please follow the same pattern used for Guass/Jacobi.

Here is the formulas for all 3 methods:

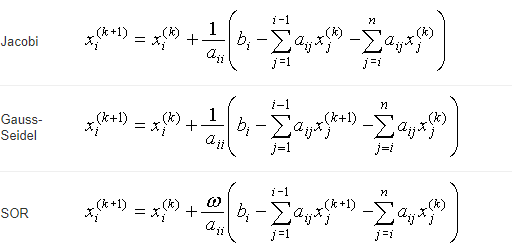
#include

#include

#include

using namespace std;

//JACOBI

void jacobi ()

{

int i, j, m, n, l;

float x[10], a[10][10], b[10], c[10];

cout

cin >> n;

cout

cin >> l;

cout

for (i = 0; i

{

cin >> b[i];

}

cout

for (i = 0; i

{

x[i] = 0;

for (j = 0; j

{

cin >> a[i][j];

}

}

m = 1;

line:

for (i = 0; i

{

c[i] = b[i];

for (j = 0; j

{

if (i != j)

{

c[i] = c[i] - a[i][j] * x[j];

}

}

}

for (i = 0; i

{

x[i] = c[i] / a[i][i];

}

m++;

if (m

{

goto line;

}

else

{

cout

for (i = 0; i

{

cout

}

}

}

//GAUSS-SAU

void gauss ()

{

int y, z, i, j, m, n, l;

float x[10], a[10][10], b[10], c;

cout

cin >> n;

cout

cin >> l;

cout

for (i = 0; i

{

cin >> b[i];

}

cout

for (i = 0; i

{

x[i] = 0;

for (j = 0; j

{

cin >> a[i][j];

}

}

m = 1;

line:

for (i = 0; i

{

c = b[i];

for (j = 0; j

{

if (i != j)

{

c = c - a[i][j] * x[j];

}

}

x[i] = c / a[i][i];

}

m++;

if (m

{

goto line;

}

else

{

cout

for (i = 0; i

{

cout

}

}

}

int

main ()

{

int i, j, m, n, l, y, z;

float x[10], a[10][10], b[10], c[10];

int input;

int stopApp;

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

bool valid;

do

{

//again:

cout

cout

cout

cout

cout

cin >> input;

switch (input)

{

case 1:

jacobi ();

break;

case 2:

gauss ();

break;

case 3:

break;

case 4:

cout

cout

cout

exit (0);

break;

default:

cout

break;

}

}

while (!valid);

}

i-1 X(k.i) = X(k) +_ | b,- av xik)-@yyk) Jacobi i-1 Gauss- Seidel -1 i-1 i-1 X(k.i) = X(k) +_ | b,- av xik)-@yyk) Jacobi i-1 Gauss- Seidel -1 i-1