Use Matlab

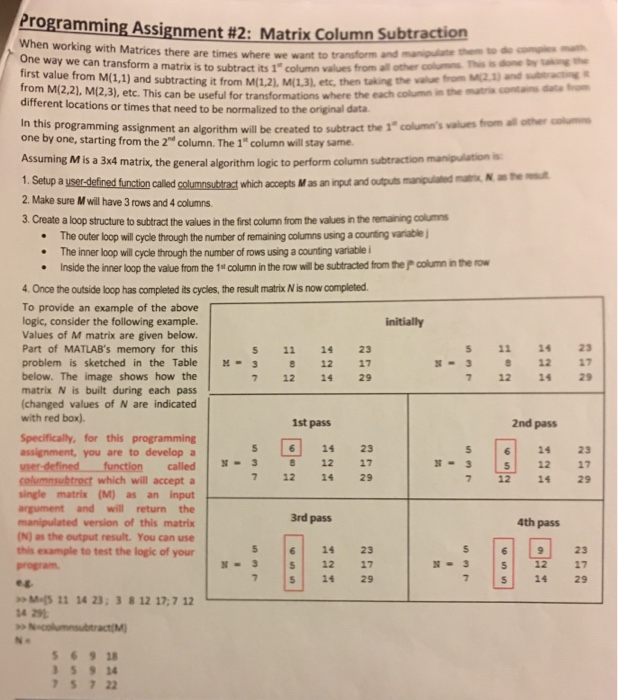
ProgrammingAssignment #2: Matrix Column Subtr When working with Matrices there are times where we want to transform One way we can transform a matrix is to subtract its 1" column values first value from M(1,1) and subtracting it from M(1.2), M(1.31, etc, then from M(2,2), M(2,3), etc. This can be usefull for transformations where different locations or times that need to be normalized to the original data manipuiate them to do comp from all other coluns taking the vale from M21)and subtracing the each column in the matria sont data In this programming assignment an algorithm will be created to subtract the 1"columa's values from all othr one by one, starting from the 2nd column. The 1* column will stay same. Assuming M is a 3x4 matrix, the general algorithm logic to perform column subtraction manaton as 1. Setup a user-defined function which 2 Make sure M will have 3 rows and 4 columns maolled "att Nus fenid called gumosubtad which accepts Mas an ngutand op 3. Create a loop structure to subtract the values in the first column from the values in the remaining columns .The outer loop will cyale through the number of remaining columns using a counting variable j The iner loop wil cycle trough the number of rows using a coning variable i Inside the inner loop the value from the 1stcolumn in the row wil be subtracted hom te olmnterow . 4. Once the outside loop has completed its cycles, the result matrix N is now completed To provide an example of the above logic, consider the following example. Values of M matrix are given below. Part of MATLAB's memory for this problem is sketched in the TableM- 3 8 12 17 below. The image shows how the matrix N is built during each pass (changed values of N are indicated with red box). 5 11 14 23 3 8 12 17 7 12 1429 5 11 14 23 7 12 14 29 1st pass 2nd pass Specificaly, for this programming assignment, you are to develop a 5 6 14 23 12 17 7 12 14 29 5 6 14 23 12 17 712 2429 3 called -3 celumnsubtrest which will accept single matrix (M) as an input argument and will return the manipulated version of this matrix N) as the output result. You can use 3rd pass 5 6 14 23 7 14 29 4th pass 23 17 7 s 14 29 this example to test the logic of your x-3151 12 17 M-t5 11 14 23:3 812 17,7 12 14 291 s6918 594 7 5 722