USE MATLAB!

USE MATLAB!

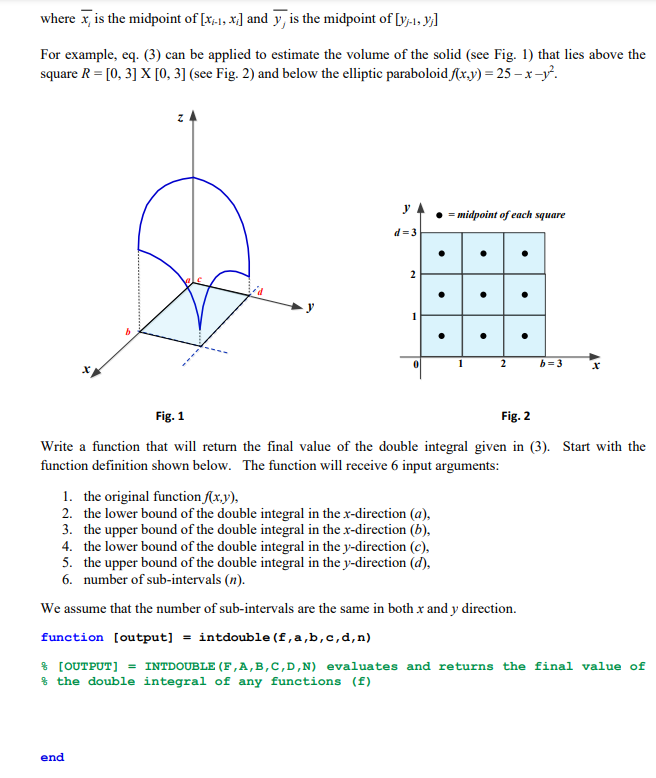
QUESTION 3: The methods that we used for approximating single integrals all have counterparts for double integrals. The Midpoint Rule for double integrals is given in the following equation. S5 f(x,y)dA=I $(4,7, hray (3) R i=1 ;=1 where x, is the midpoint of [X-1, xi] and y, is the midpoint of [yj-1, y;] For example, eq. (3) can be applied to estimate the volume of the solid (see Fig. 1) that lies above the square R = [0, 3] x [0, 3] (see Fig. 2) and below the elliptic paraboloid f(x,y)= 25 x-y? Y = midpoint of each square d=3 . 2 b=3 Fig. 1 Fig. 2 Write a function that will return the final value of the double integral given in (3). Start with the function definition shown below. The function will receive 6 input arguments: 1. the original function f(x,y), 2. the lower bound of the double integral in the x-direction (a), 3. the upper bound of the double integral in the x-direction (b), 4. the lower bound of the double integral in the y-direction (C), 5. the upper bound of the double integral in the y-direction (d), 6. number of sub-intervals (n). We assume that the number of sub-intervals are the same in both x and y direction. function (output] = intdouble (f, a,b,c,d,n) $ (OUTPUT] = INTDOUBLE (F,A,B,C,D,N) evaluates and returns the final value of % the double integral of any functions (E) end To evaluate the function, you can define a function for the elliptic paraboloid, as given below: function [z] = elliptic(x,y) z = 25-x^2-2*y^2; end Then in the Command Window: >> intdouble (@elliptic,0,3,0,3,3) ans = 146.2500