Use of the Problem Solving Process is not necessary for this problem as I am giving you most of the necessary Java code. Additionally, I have provided below, sample code segments that can be used to measure the processing time of each algorithm. Note: You will need to modify this code to meet your needs.

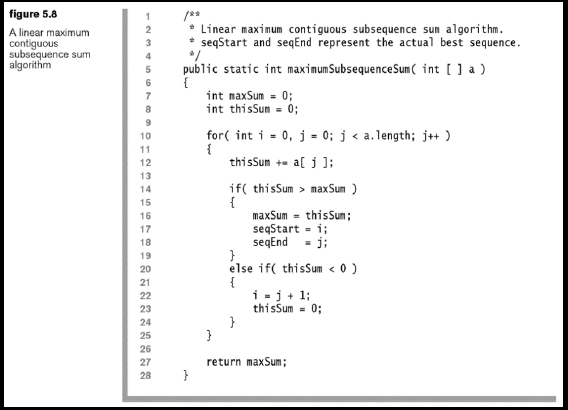
Please use The Cubic maximum contiguous subsequence sum algorithm (figure 5.4), the Quadratic maximum contiguous subsequence sum algorithm (figure 5.5), and the linear maximum contiguous subsequence sum algorithm (figure 5.8) to create one single application that compares the processing times of each algorithm against the same array of numbers.

The application needs to be run with and array of ten (10), twenty (20), fifty (50), one hundred (100) and two hundred (200)random integers with the range of integers between -10 to 10. Note: The code can be modified between runs to account for the change in array size.

SAMPLE CODE FOR TIME OF EXECUTION: // one way to process execution time of a method long startTime1 = System.nanoTime(); FirstMethodToTime(); long startTime2 = System.nanoTime(); SecondMethodToTime(); long endTimeAll = System.nanoTime();

long duration2ndMethod = (endTime startTime2); //divide by 1000000 for milliseconds.

long duration2ndMethod = (startTime2 startTime1); //divide by 1000000 milliseconds.

// Another way to process execution time of a method long startTime = System.currentTimeMillis(); FirstMethodToTime();; long endTime = System.currentTimeMillis(); System.out.println("That took " + (endTime - startTime) + " milliseconds")

An Array demonstration can be usefull

2 Cubic naxinun contiguous subsequence sun algorithn. seq Start and seqEnd re present the actual best sequence 5 public static int maxSubsequenceSum int 1 a) int naxSun o; for( int i 0; i a.length; i for int j i: j a.length; j++) 10 11 int this Sun 0; 12 for int k i: k j; k++) 14 this Sun a[ k 15 16 if( thisSun maxSum 18 maxSun thisSum 19 seqStart i: seqEnd j; 21 24 return maxSum 26 figure 5.4 A cubic maximum contiguous subsequence sum algorithm