USE ONLY JAVA! Here is the output: 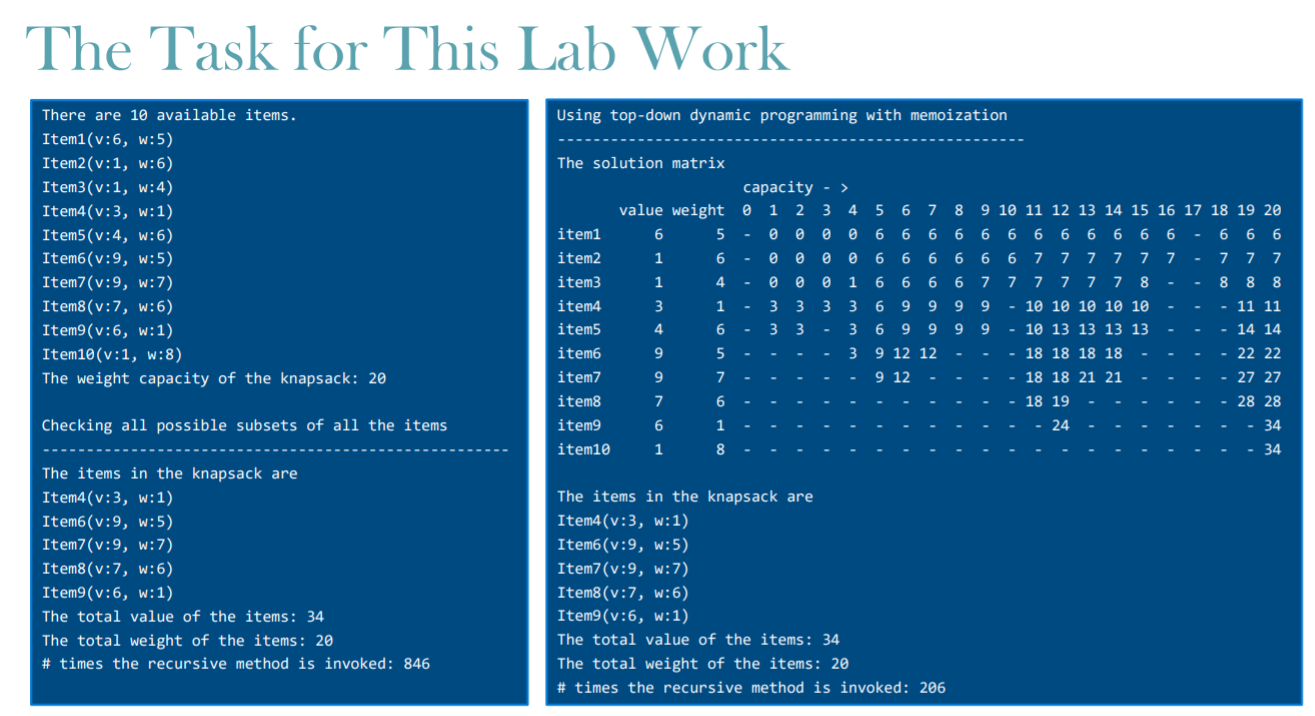I need only "knapsackMemoization" method and "PrintSolution" Method. Here is the implementation algorithm for knapsackMemoization method.

Here is the given code. Remember, I need only knapsackMemoization(int n, int capacity) method and printSolution() method.

import java.util.ArrayList; // A template to implement and demonstrate a recursive method based on top-down // dynamic programming with memoization for solving the 0-1 knapsack problem and // compare this method with the basic recursive method that checks all possible // item subsets in terms of the number of the invocations for a single call. public class Lab12Template { // a 2-D array to store the values and the weights of all the available items private static int[][] items; // 2 counters to demonstrate the efficiency of memoization on the same problem // count1 -> how many times the method without memoization is invoked // count2 -> how many times the method with memoization is invoked private static int count1 = 0, count2 = 0; // solves the 0-1 knapsack problem recursively by checking all possible item // subsets and returns an array list that stores the total value of the items // put into the knapsack followed by the indexes of these items private static ArrayList knapsack(int n, int capacity) { // increase the counter that stores how many times this method is invoked count1++; // base case: the number of the available items or the capacity is zero if (n == 0 || capacity == 0) { // create and return an array list that contains a single element zero // as the total value of the items put into the knapsack ArrayList knapsack = new ArrayList(); knapsack.add(0); return knapsack; } // test the last available item int index = n - 1, value = items[index][0], weight = items[index][1]; // linear recursive case: the weight of the item exceeds the capacity if (weight > capacity) // return the output of the knapsack method excluding the item return knapsack(n - 1, capacity); // binary recursive case (compare 2 possibilities: one when the item is not // put in the knapsack and the other when the item is put in the knapsack) ArrayList knapsack1 = knapsack(n - 1, capacity); ArrayList knapsack2 = knapsack(n - 1, capacity - weight); knapsack2.add(index); knapsack2.set(0, knapsack2.get(0) + value); // return the knapsack with greater total value between the 2 possibilities if (knapsack1.get(0) >= knapsack2.get(0)) return knapsack1; else return knapsack2; } // a 2-D array to store the maximum possible total value for each computed // subproblem (used for memoization) private static Integer[][] solution; // solves the 0-1 knapsack problem recursively by using an approach based on // top-down dynamic programming with memoization (fills and uses the solution // matrix as needed to prevent repeated computations for any subproblem) and // returns the total value of the items put into the knapsack private static int knapsackMemoization(int n, int capacity) { // Write the body of this method }  // prints the solution of the 0-1 knapsack problem (used for the 2nd approach // which is based on top-down dynamic programming with memoization)  private static void printSolution(boolean printSolutionMatrix) { // get the number of all the items and the weight capacity of the knapsack int numItems = solution.length, capacity = solution[0].length - 1; // print the solution matrix if printSolutionMatrix is given as true if (printSolutionMatrix) { System.out.println("The solution matrix"); // print the header System.out.println(" capacity - >"); System.out.print(" value weight "); for (int c = 0; c = 0; i--) { // the current item is in the solution if its index is zero (and there // is some remaining total value) or the value at the previous row in // the solution matrix is different from the remaining total value if (i == 0 || solution[i - 1][capacity] != totalValue) { // add the current item to the knapsack string from the left int index = i + 1, v = items[i][0], w = items[i][1]; knapsack = " Item" + index + "(v:" + v + ", w:" + w + ")" + knapsack; // compute the remaining total value and the remaining capacity by // excluding the current item totalValue -= v; capacity -= w; // add the weight of the current item to the total weight to print totalWeight += w; // if the remaining total value or the remaining capacity becomes 0 if (totalValue == 0 || capacity == 0) break; // no need to check the remaining items -> end the loop } } // print the resulting knapsack string System.out.println(knapsack); // print the total value and the total weight of the items in the knapsack capacity = solution[0].length - 1; totalValue = solution[numItems - 1][capacity]; System.out.println("The total value of the items: " + totalValue); System.out.println("The total weight of the items: " + totalWeight); } // generates random integers in the range [1, 9] for the value and the weight // of each item, stores them in a 2-D array, uses both the recursive knapsack // method that checks all possible item subsets and the knapsackMemoization // method that is based on top-down dynamic programming with memoization for // solving the same 0-1 knapsack problem defined by the weight capacity 20 and // 10 random items, counts the number of the times these methods are invoked // recursively, and prints the results on the console public static void main(String[] args) { // there are 10 items and the weight capacity of the knapsack is 20 kgs int numItems = 10, weightCapacity = 20; // create the 2-D items array to store a value and a weight for each item items = new int[numItems][2]; // create random integers in the range [1, 9] for the value and the weight // of each item and store them in the items array while printing the items System.out.println("There are " + numItems + " available items."); for (int i = 0; i  knapsack = knapsack(numItems, weightCapacity); // print the solution on the console System.out.println("The items in the knapsack are "); int totalValue = knapsack.get(0); int totalWeight = 0; for (int k = 1; k NOTE: Please do not write unrelated answers like repeatCharNTimes ( int n,char ch), yorknacci(int n) or numberOfFirstChar(String st ).  I would like to get only the correct answer. Also as I said, do not use C or C++, use Java please.

. . o Examine the given Lab12Template class (Lab12Template.java). Your task is to modify the two methods given with the following headers in this class: o private static int knapsackMemoization (int n, int capacity) o private static void printSolution(boolean printSolution Matrix) Write the body of the given knapsackMemoization method such that o it implements top-down dynamic programming with memoization as explained in the slides 12 and 13. o and it counts the number of the times the method is invoked recursively by using count2. The given printSolution method prints the solution of the 0-1 knapsack problem as shown in the slide 33. Modify this method such that it can deal with the empty values in the solution matrix as in the given example console output in the next slide. Note: When top-down dynamic programming with memoization is used, some values in the solution matrix remain with their default values (here the default value is null as the matrix has the type Integer) as the solution for the corresponding subproblems are not computed. This is due to the fact that some subproblems do not exist in practice and we are using a top-down approach not a bottom-up approach. The Task for This Lab Work Using top-down dynamic programming with memoization There are 10 available items. Item1(v:6, w:5) Item2(v:1, w:6) Item3(v:1, w:4) Item4(v:3, w:1) Item5(v:4, w:6) Item6(v:9, w:5) Item7(v:9, w:7) Item8(v:7, w:6) Item(v:6, w:1) Item10(v:1, w:8) The weight capacity of the knapsack: 20 - The solution matrix capacity - > value weight 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 item1 6 5 Looo 0 6 6 6 6 6 6 6 6 6 6 6 6 - 6 6 6 item2 1 6 . 0 0 0 6 6 6 6 6 6 7 7 7 7 7 7 . 7 7 7 item3 1 4 - 0 0 0 1 6 6 6 6 7 7 7 7 7 7 8 8 8 8 item4 3 1 - 3 3 3 3 6 9 9 9 9 - 10 10 10 10 10 - 11 11 item5 4 6 3 3 - 3 6 9 9 9 9 - 10 13 13 13 13 14 14 item6 9 5 3 9 12 12 - 18 18 18 18 22 22 item7 9 7 9 12 18 18 21 21 27 27 item8 7 6 18 19 28 28 item9 6 1 - 24 - 34 item10 1 8 34 Checking all possible subsets of all the items The items in the knapsack are Item4(v:3, w:1) Item(v:9, w:5) Item(v:9, w:7) Item8(v:7, w:6) Item(v:6, w:1) The total value of the items: 34 The total weight of the items: 20 # times the recursive method is invoked: 846 The items in the knapsack are Item4(v:3, w:1) Item6(v:9, w:5) Item(v:9, w:7) Items (v:7, w:6) Item(v:6, w:1) The total value of the items : 34 The total weight of the items: 20 # times the recursive method is invoked: 206 Top-down Dynamic Programming with Memoization . The recursive algorithm given below finds and returns the total value of the items put into the knapsack in the optimal solution by checking all possible subsets of all the items. Algorithm Knapsack(n, W): Input: The number of the items (n) and an integer weight capacity (W) Output: The total value of the items put into the knapsack in the solution if n = 0 or W = 0 then return 0 if w, > W then return Knapsack(n - 1, W) totalValue1 = Knapsack(n - 1, W) totalValue2 = vn + Knapsack(n - 1, W - w.) return max(totalValue1, totalValue2) The algorithm given below is a modified version of the basic recursive algorithm given on the left side. It implements a top-down dynamic programming approach with memoization. Algorithm KnapsackMemoization(n, W): Input: The number of the items (n) and an integer weight capacity (W) Output: The total value of the items put into the knapsack in the solution if n = 0 or W = 0 then return 0 if solution[n - 1][W] = null then return solution[n - 1][W] if w, > W then solution[n - 1][W] = KnapsackMemoization(n - 1, W) return solution[n - 1][W] totalValue1 = KnapsackMemoization(n - 1, W) totalValue2 = vn + KnapsackMemoization(n - 1, W - wn) solution[n - 1][W] = max(totalValue1, totalValue2) return solution[n - 1][W] =