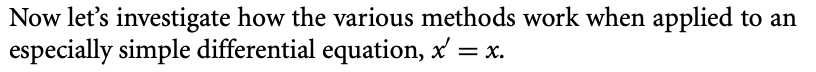
use python to do from e to h

Now let's investigate how the various methods work when applied to an especially simple differential equation, x=x (b) Use Euler's method to approximate the value of x(1)=e using the step size t=0.1. That is, recursively determine tk and xk for k= 1,,10 using t=0.1 and starting with t0=0 and x0=1. (c) Repeat the previous step with t half the size, namely 0.05 . (d) Again use Euler's method, this time reducing the step size by a factor of 5 , so that t=0.01 to approximate x(1). (e) Repeat the previous three steps using the Improved Euler's method with the same step sizes. (f) Repeat using Runge-Kutta. (g) You now have nine different approximations for the value of x(1)=e, three for each method. Calculate the error in each case. For the record, use the value e=2.71828182845235360287 in calculating the error. (h) Calculate how the error changes as you change the step size from 0.1 to 0.05 and then from 0.05 to 0.01 . That is, if denotes the error made using step size , compute both 0.1/0.05 and 0.05/0.01