Use python!

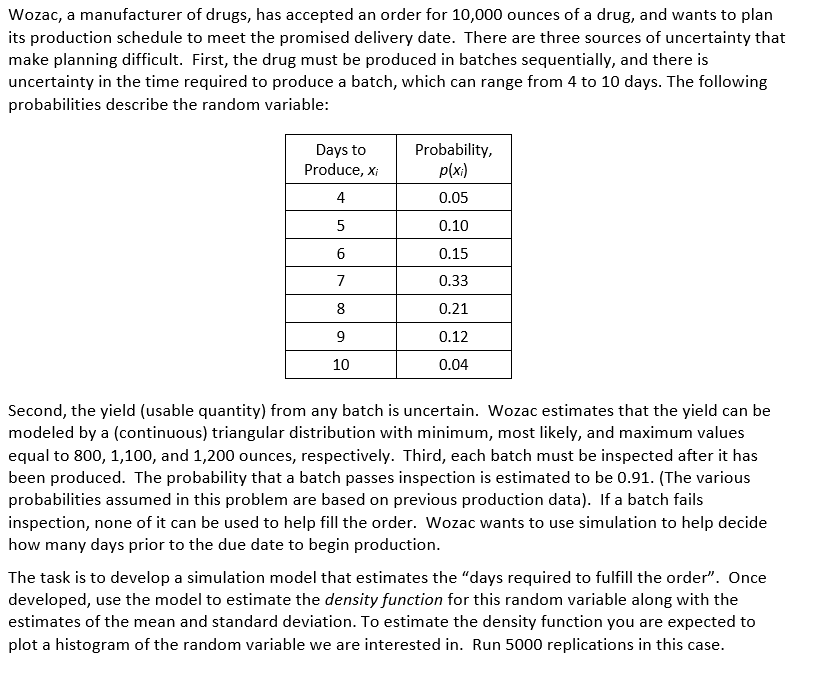
Wozac, a manufacturer of drugs, has accepted an order for 10,000 ounces of a drug, and wants to plan its production schedule to meet the promised delivery date. There are three sources of uncertainty that make planning difficult. First, the drug must be produced in batches sequentially, and there is uncertainty in the time required to produce a batch, which can range from 4 to 10 days. The following probabilities describe the random variable Probability, p(x) 0.05 0.10 0.15 0.33 0.21 0.12 0.04 Days to Produce, Xi 4 10 Second, the yield (usable quantity) from any batch is uncertain. Wozac estimates that the yield can be modeled by a (continuous) triangular distribution with minimum, most likely, and maximum values equal to 800, 1,100, and 1,200 ounces, respectively. Third, each batch must be inspected after it has been produced. The probability that a batch passes inspection is estimated to be 0.91. (The various probabilities assumed in this problem are based on previous production data). If a batch fails inspection, none of it can be used to help fill the order. Wozac wants to use simulation to help decide how many days prior to the due date to begin production The task is to develop a simulation model that estimates the "days required to fulfill the order". Once developed, use the model to estimate the density function for this random variable along with the estimates of the mean and standard deviation. To estimate the density function you are expected to plot a histogram of the random variable we are interested in. Run 5000 replications in this case. Wozac, a manufacturer of drugs, has accepted an order for 10,000 ounces of a drug, and wants to plan its production schedule to meet the promised delivery date. There are three sources of uncertainty that make planning difficult. First, the drug must be produced in batches sequentially, and there is uncertainty in the time required to produce a batch, which can range from 4 to 10 days. The following probabilities describe the random variable Probability, p(x) 0.05 0.10 0.15 0.33 0.21 0.12 0.04 Days to Produce, Xi 4 10 Second, the yield (usable quantity) from any batch is uncertain. Wozac estimates that the yield can be modeled by a (continuous) triangular distribution with minimum, most likely, and maximum values equal to 800, 1,100, and 1,200 ounces, respectively. Third, each batch must be inspected after it has been produced. The probability that a batch passes inspection is estimated to be 0.91. (The various probabilities assumed in this problem are based on previous production data). If a batch fails inspection, none of it can be used to help fill the order. Wozac wants to use simulation to help decide how many days prior to the due date to begin production The task is to develop a simulation model that estimates the "days required to fulfill the order". Once developed, use the model to estimate the density function for this random variable along with the estimates of the mean and standard deviation. To estimate the density function you are expected to plot a histogram of the random variable we are interested in. Run 5000 replications in this case