3). Your answer from part (2) can be thought of as an area function, Alx), which measures the area under the graph from t 1 to t x. Find A(4) using this function. How does this value compare to your calculation in part (1)??

4). Use the area function A(x) to find A(1). What does this represent geometrically? 4.?

5). Use the area function Alx) to find the area from x 3 to x 6 5.?

6. Use the area function A(x) to find the area from x 0 to x3.?

7). How can we determine an expression for the rate of change of this function A (x)? Find this expression.?

8). What is the relationship between the area function A(x) and the original function in our graph, f (t)??

9). Use the area function A(x) to find the area from x 1 to x 0. 9. b. 1 to x?

10). Use the area function Alx) to find the area from x?

11). Assuming that a

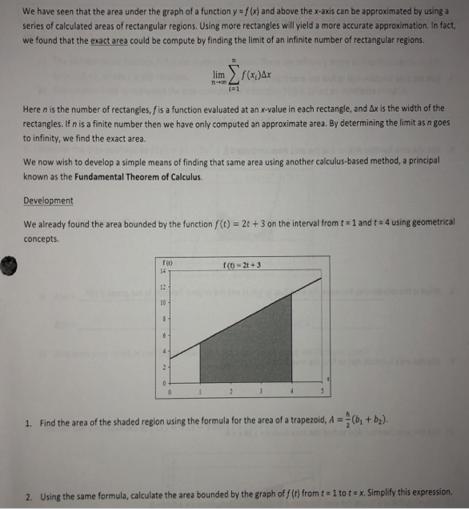
We have seen that the area under the graph of a function y=f(x) and above the x-axis can be approximated by using a series of calculated areas of rectangular regions. Using more rectangles will yield a more accurate approximation. In fact, we found that the exact area could be compute by finding the limit of an infinite number of rectangular regions. lim (01 f(x,)&x Heren is the number of rectangles, fis a function evaluated at an x-value in each rectangle, and Ax is the width of the rectangles. If n is a finite number then we have only computed an approximate area. By determining the limit as n goes to infinity, we find the exact area. 100 14 13 We now wish to develop a simple means of finding that same area using another calculus-based method, a principal known as the Fundamental Theorem of Calculus Development We already found the area bounded by the function f(t)= 2: +3 on the interval from t = 1 and t = 4 using geometrical concepts. 1(0-21+3 1. Find the area of the shaded region using the formula for the area of a trapezoid, A= (b + b). 2. Using the same formula, calculate the area bounded by the graph of f(t) from t = 1 totex. Simplify this expression.