A rotating electric dipole can be thought of as the superposition of two oscillating dipoles, one along
Question:
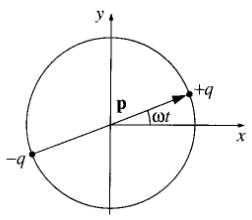
A rotating electric dipole can be thought of as the superposition of two oscillating dipoles, one along the x axis, and the other along the y axis (Fig. 11.7), with the latter out of phase by 90o: p = p0[cos(wt) x + sin(wt) y]. Using the principle of superposition and Eqs 11.18 and 11.19 (perhaps in the form suggested by Prob. 11.2), find the fields of a rotating dipole. Also find the Poynting vector and the intensity of the radiation. Sketch the intensity profile as a function of the polar angle θ, and calculate the total power radiated. Does the answer seem reasonable? (Note that power, being quadratic in the fields, does not satisfy the superposition principle. In this instance, however it seems to. Can you account for this?)
Step by Step Answer:
By the superposition principle we can add the potentials of the two dipoles Lets first express V Eq ...View the full answer
