Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Use the definitions bar{x} =(1)/(n)sum x_(i) and s_(x)^(2)=(1)/(n)sum (x_(i)-(bar{x} ))^(2) to show that if Y_(i)= a+bx_(i) , then (a) /bar (Y)=a+bbar{x} and s_(Y)^(2)=(1)/(n)sum (Y_(i)-(/bar
Use the definitions
\\\\bar{x} =(1)/(n)\\\\sum x_(i)and
s_(x)^(2)=(1)/(n)\\\\sum (x_(i)-(\\\\bar{x} ))^(2)to show that if
Y_(i)=\
a+bx_(i), then\ (a)
/bar (Y)=a+b\\\\bar{x} and
s_(Y)^(2)=(1)/(n)\\\\sum (Y_(i)-(/bar (Y)))^(2)=b^(2)s_(x)^(2); (3 pts)\ (b) If
Z_(i)=(x_(i)-(\\\\bar{x} ))/(s_(x)), then
/bar (Z)=0and
s_(z)^(2)=1.(3pts) 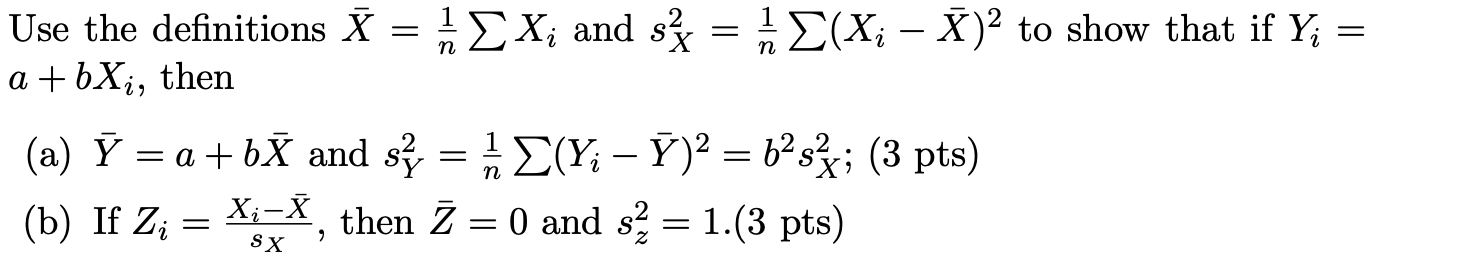
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


