Use the link in the Jupyter Notebook activity to access your Python script. Once you have made your calculations, complete discussion. The script will output answers to the questions given below. You must attach your Python script output as an HTML file and respond to the questions below.

In this discussion, you apply the statistical concepts and techniques covered in this week's reading about one-way analysis of variance (ANOVA). An investment analyst is evaluating the 10-year mean return on investment for industry-specific exchange-traded funds (ETFs) for three sectors: financial, energy, and technology. The analyst obtains a random sample of 30 ETFs for each sector and calculates the 10-year return of each ETF. The analyst has provided you with this data set. Run Step 1 in the Python script to upload the data file.

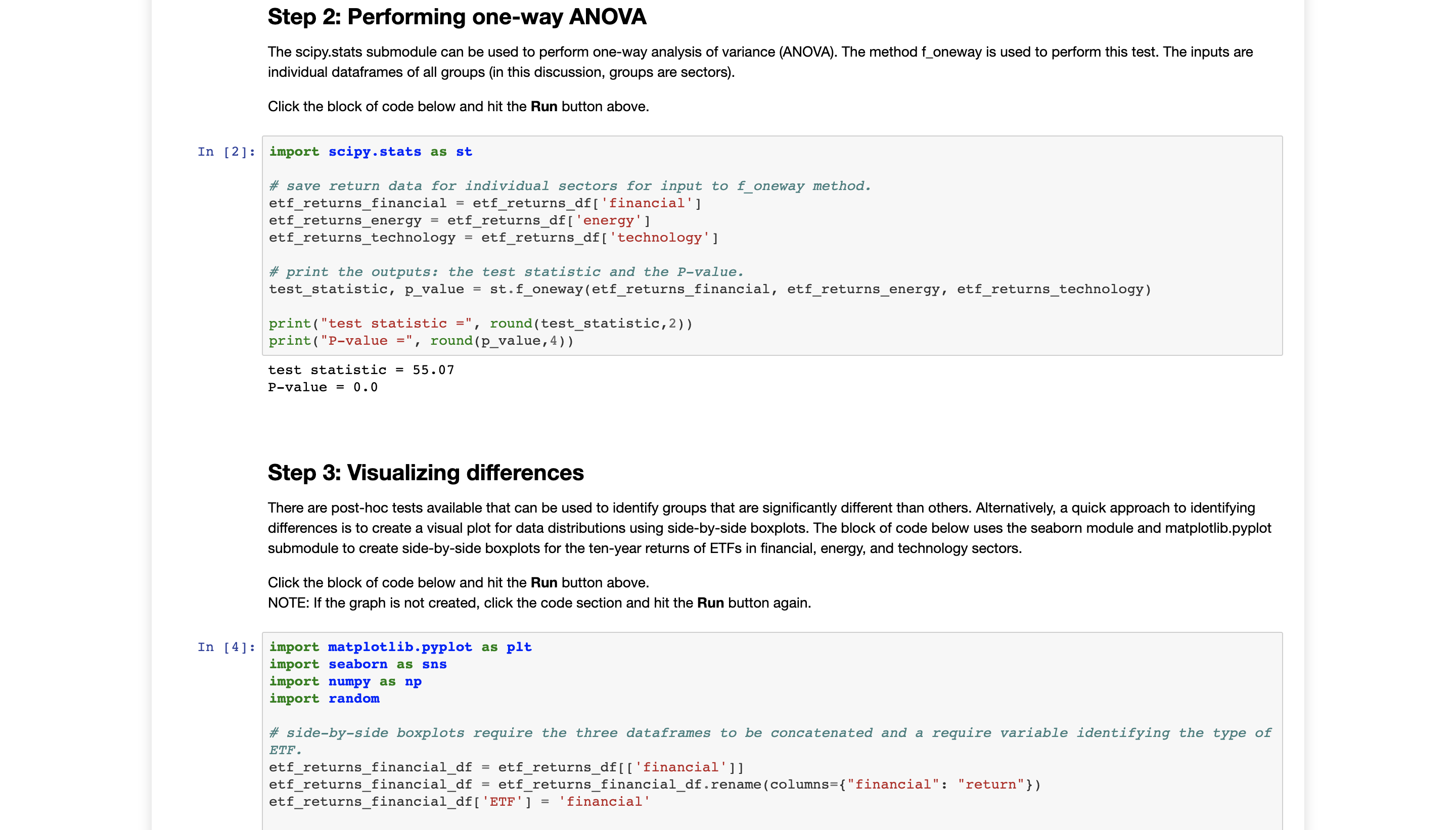
Using the sample data, perform one-way analysis of variance (ANOVA). Evaluate whether the average return ofat least oneof the industry-specific ETFs is significantly different. Use a 5% level of significance.

In your initial post, address the following items:

1. Define the null and alternative hypothesis in mathematical terms and in words.
2. Report the level of significance.
3. Include the test statistic and the P-value. See Step 2 in the Python script.
4. Provide your conclusion and interpretation of the test. Should the null hypothesis be rejected? Why or why not?
5. Does a side-by-side boxplot of the 10-year returns of ETFs from the three sectors confirm your conclusion of the hypothesis test? Why or why not? See Step 3 in the Python script.

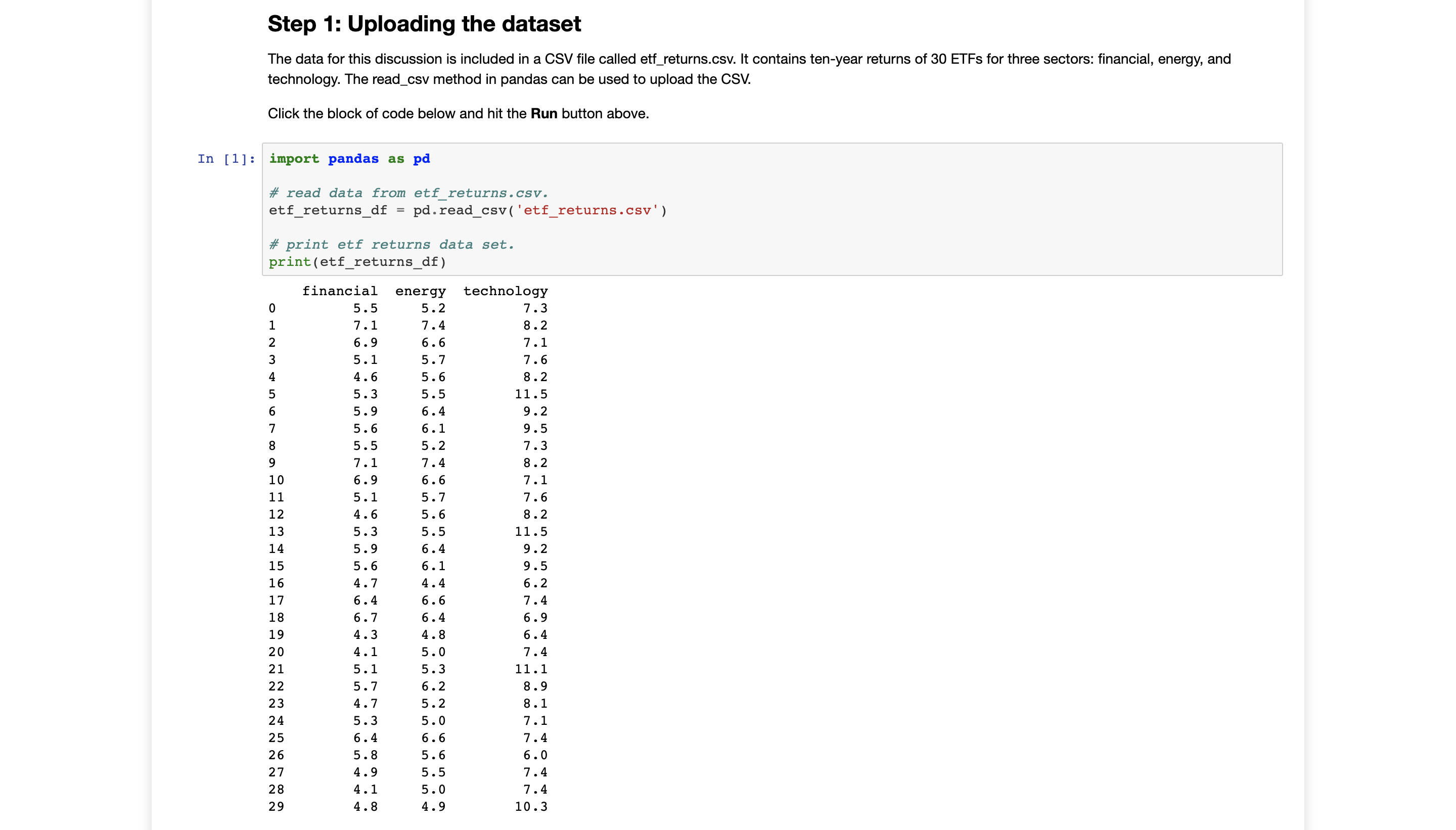
Step 1: Uploading the dataset The data for this discussion is included in a CSV file called etf_returns.csv. It contains ten-year returns of 30 ETFs for three sectors: financial, energy, and technology. The read_csv method in pandas can be used to upload the CSV. Click the block of code below and hit the Run button above. In [1] : import pandas as pd # read data from etf_returns. csv. etf_returns_df = pd. read_csv( 'etf_returns.csv' ) # print etf returns data set. print (etf_returns_df) financial energy technology 5.5 5. 2 7.3 7. 1 7. 4 B . 2 6.9 6.6 7.1 5 . 1 5 . 7 7.6 4 . 6 5 . 6 8 . 2 5 .3 5 .5 11.5 5 .9 6. 4 9 . 2 5 . 6 6. 1 9.5 5 .5 5 . 2 7.3 7 . 1 7.4 8 . 2 10 6.9 6.6 7.1 11 5 . 1 5 . 7 7. 6 12 4. 6 5 .6 8 . 2 13 5 . 3 5 .5 11.5 14 5 .9 6. 4 9 . 2 15 5 . 6 6.1 9.5 16 4.7 4.4 6. 2 17 6. 4 6. 6 7.4 18 6.7 6.4 6.9 19 4.3 4.8 6. 4 20 4. 1 5.0 7. 4 21 5 . 1 5 .3 11 . 1 22 5 . 7 6.2 8. 9 23 4. 7 5 . 2 8. 1 24 5 . 3 5 .0 7. 1 25 6. 4 6 .6 7. 4 26 5 . 8 5 . 6 6.0 27 4.9 5.5 7. 4 28 4.1 5.0 7. 4 29 4.8 4.9 10.3Step 2: Performing one-way ANOVA The scipy.stats submodule can be used to perform one-way analysis of variance (ANOVA). The method f_oneway is used to perform this test. The inputs are individual dataframes of all groups (in this discussion, groups are sectors). Click the block of code below and hit the Run button above. In [2]: import scipy . stats as st # save return data for individual sectors for input to f_oneway method. etf_returns_financial = etf_returns_df[ ' financial' ] etf_returns_energy = etf_returns_df [ 'energy' ] etf_returns_technology = etf_returns_df[ 'technology' ] # print the outputs: the test statistic and the P-value. test_statistic, p_value = st. f_oneway (etf_returns_financial, etf_returns_energy, etf_returns_technology) print ("test statistic =", round(test_statistic, 2) ) print ( "P-value =", round(p_value, 4) ) test statistic = 55. 07 P-value = 0.0 Step 3: Visualizing differences There are post-hoc tests available that can be used to identify groups that are significantly different than others. Alternatively, a quick approach to identifying differences is to create a visual plot for data distributions using side-by-side boxplots. The block of code below uses the seaborn module and matplotlib.pyplot submodule to create side-by-side boxplots for the ten-year returns of ETFs in financial, energy, and technology sectors. Click the block of code below and hit the Run button above. NOTE: If the graph is not created, click the code section and hit the Run button again. In [4]: import matplotlib. pyplot as plt import seaborn as sns import numpy as np import random # side-by-side boxplots require the three dataframes to be concatenated and a require variable identifying the type of ETF. etf_returns_financial_df = etf_returns_df[ [ ' financial' ] ] etf_returns_financial_df = etf_returns_financial_df . rename (columns={ "financial": "return"} ) etf_returns_financial_df [ 'ETF' ] = 'financial'In [4] : import matplotlib. pyplot as pit import seaborn as sns import numpy as np import random # side-by-side boxplots require the three dataframes to be concatenated and a require variable identifying the type of ETF. etf_returns_financial_df = etf_returns_df [ [ ' financial' ] ] etf_returns_financial_df = etf_returns_financial_df . rename (columns={ "financial": "return"}) etf_returns_financial_df [ 'ETF' ] = 'financial' etf_returns_energy_df = etf_returns_df [ [' energy' ] ] etf_returns_energy_df = etf_returns_energy_df . rename (columns={"energy": "return"}) etf_returns_energy_df [ 'ETF' ] = 'energy etf_returns_technology_df = etf_returns_df [ [ 'technology' ] ] etf_returns_technology_df = etf_returns_technology_df . rename (columns={ "technology": "return"}) etf_returns_technology_df [ 'ETF' ] = 'technology' # concatenate dataframes for the three ETFs. all_etfs_df = pd. concat ( (etf_returns_financial_df, etf_returns_energy_df, etf_returns_technology_df) ) # set a title for the plot, x-axis, and y-axis. pit. title( 'Boxplot for comparison', fontsize=20) # prepare the boxplot. sns . boxplot (x="ETF" , y="return" , data=all_etfs_df) # show the plot. plt . show ( ) Boxplot for comparison 11 10 9 8 return V UT financial energy technology ETF