use these methods :

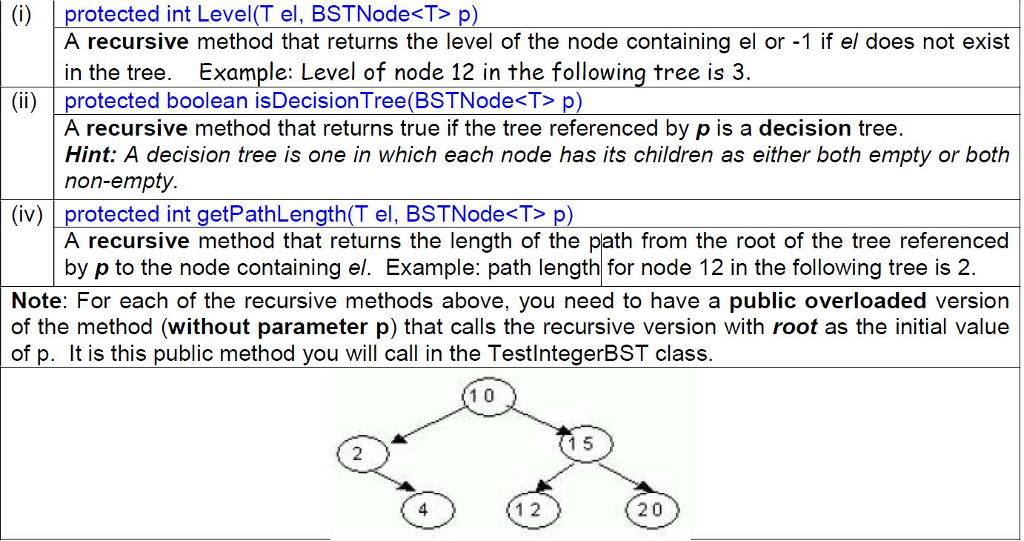
public int level(T el) { return level(el, root); } protected int level(T el, BSTNode p) { if(p == null) { return -1; } if(p.key.equals(el)) { return 1; } int l = level(el, p.left); int r = level(el, p.right); if(l != -1) { return 1 + l; } else if(r != -1) { return 1 + r; } else { return -1; } } 

this A recursive method that returns the level of the node containing el or -1 if el does not exist in the tree. Example: Level of node 12 in the following tree is 3.

----------------------------------------------------------------------------------------------------------------------------

public boolean isDecisionTree() { return isDecisionTree(root); } protected boolean isDecisionTree(BSTNode p) { if(p == null || (p.left == null && p.right == null)) { return true; } else if(p.left != null && p.right != null){ return isDecisionTree(p.left) && isDecisionTree(p.right); } else { return false; } } 

this

A recursive method that returns true if the tree referenced by p is a decision tree. Hint: A decision tree is one in which each node has its children as either both empty or both non-empty.

-----------------------------------------------------------------------------------------------------------------------------------

public int getPathLength(T el) { return getPathLength(el, root); } protected int getPathLength(T el, BSTNode p) { if(p == null) { return -1; } if(p.key.equals(el)) { return 0; } int l = getPathLength(el, p.left); int r = getPathLength(el, p.right); if(l != -1) { return 1 + l; } else if(r != -1) { return 1 + r; } else { return -1; } }

this A recursive method that returns the length of the path from the root of the tree referenced by p to the node containing el. Example: path length for node 12 in the following tree is 2.

------------------------------------------------------------------------------------------------------------------------------

add new case in this class to test these methods :

import java.util.Scanner;

import java.util.*;

public class TestIntegerBST {

public static void main (String[] args){

BST tree = new BST();

int option, target;

Scanner reader = new Scanner(System.in);

do {

System.out.println(" ***************************");

System.out.println("* Testing Binary Search Tree *");

System.out.println("*************************** ");

System.out.println("1. Insert an element");

System.out.println("2. Search for an element");

System.out.println("3. Delete an element");

System.out.println("4. Print in Breadth-First-Order");

System.out.println("5. Print in Pre-Order");

System.out.println("6. Print in In-Order");

System.out.println("7. Print in Post-Order");

System.out.println("8. Print sum of the elements");

System.out.println("9. Quit");

System.out.print(" Select an Option [1...9] : ");

option = reader.nextInt();

switch (option) {

case 1 : System.out.print("Enter the element to insert: ");

tree.insert(reader.nextInt());

break;

case 2 : System.out.print("Enter the element to search for: ");

target = reader.nextInt();

Integer result = tree.search(target);

if (result != null)

System.out.println("Element, "+result+ " was found in the tree");

else

System.out.println("Sorry, the element was not found");

break;

case 3 : System.out.print("Enter the element delete: ");

tree.delete(reader.nextInt());

break;

case 4 : tree.breadthFirst();

break;

case 5 : tree.preorder();

break;

case 6 : tree.inorder();

break;

case 7 : tree.postorder();

break;

case 8 : System.out.print("Sum of the elements in the tree is: "+sum(tree));

break;

} //end of switch

} while (option != 9);

} //end of main

public static int sum(BST tree) {

int sum = 0;

for (int n : tree)

sum += n;

return sum;

}

}

(i) protected int Level(T el, BSTNode T> p) A recursive method that returns the level of the node containing el or -1 if el does not exist in the tree. Example: Level of node 12 in the following tree is 3. (ii) protected boolean isDecision Tree(BSTNode A recursive method that returns true if the tree referenced by p is a decision tree. Hint: A decision tree is one in which each node has its children as either both empty or both non-empty (iv) protected int getPathLength(T el, BSTNode A recursive method that returns the length of the path from the root of the tree referenced by p to the node containing el. Example: path length for node 12 in the following tree is 2. Note: For each of the recursive methods above, you need to have a public overloaded version of the method (without parameter p) that calls the recursive version with root as the initial value of p. It is this public method you will call in the TestlntegerBST class. 1 0 1 5 2 1 2 20