Using C++, write a class for complex numbers. A complex number has the form a + bi, where "a" and "b" are real numbers and i is the square root of -1. We refer to "a" the real part and "b" as the imaginary part of the number. The class should have two data members to represent the real and imaginary numbers; the constructor takes two arguments to set these members. Discuss and implement other appropriate operators for this class. Create complex_number.cpp using the header file complex_number.h and the test program test_complex.cpp.

complex_number.h

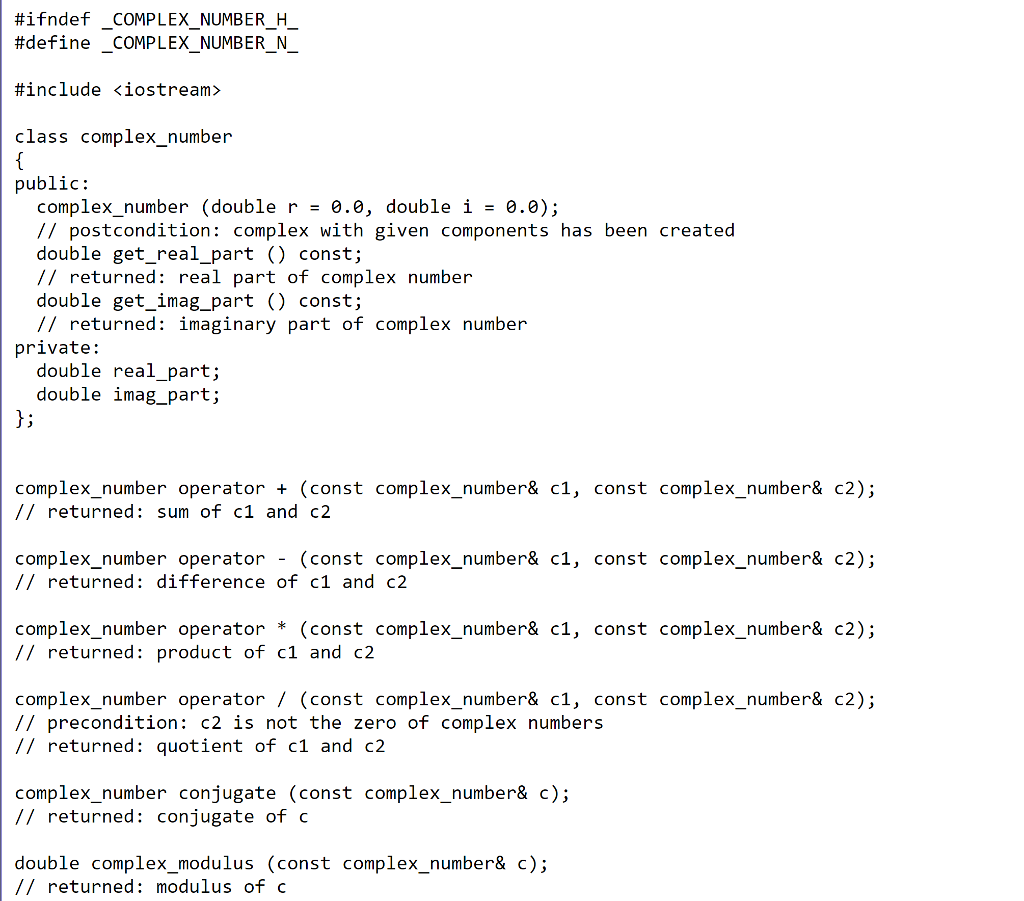
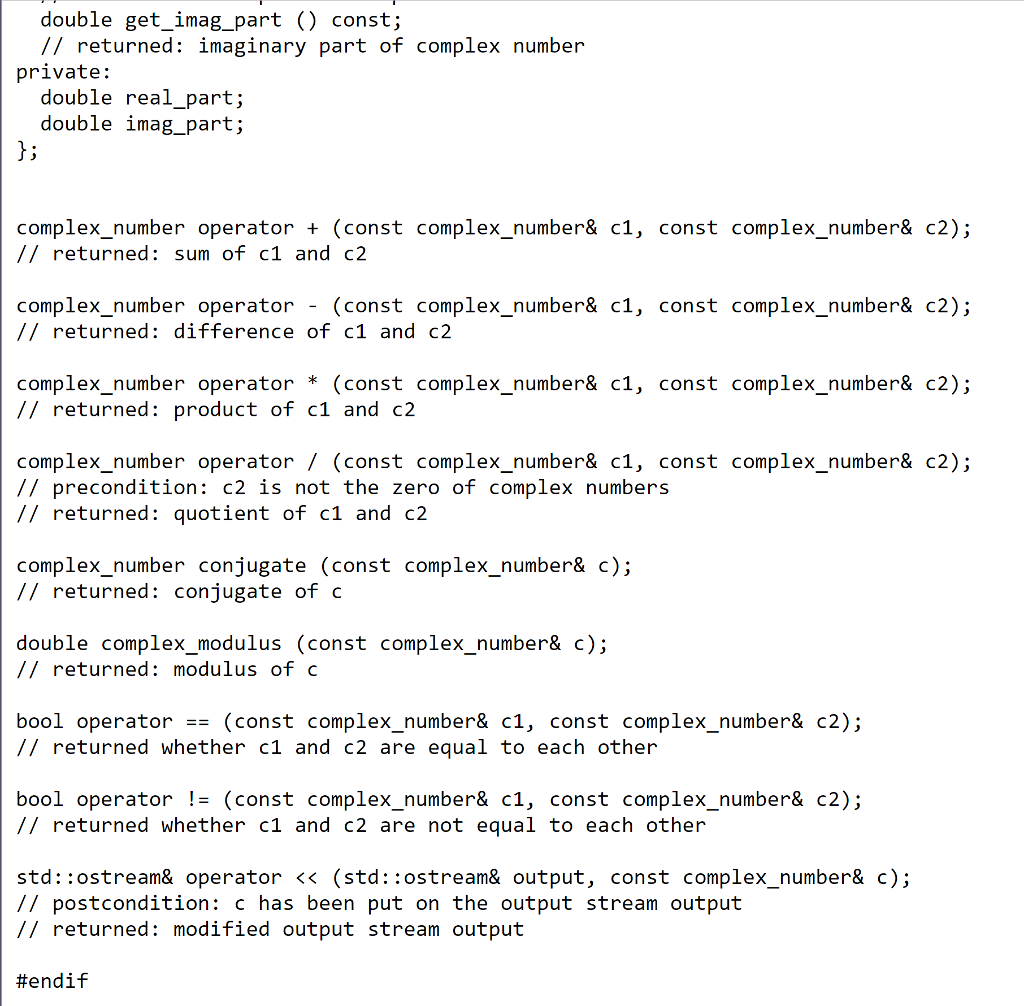
test_complex.cpp

#ifndef COMPLEX NUMBER H #define COMPLEX NUMBER N #include iostream class complex number public: complex_number (double r-0.0, double i-0.0); // postcondition: complex with given components has been created double get real part const // returned: real part of complex number double get_imag_part () const; // returned: imaginary part of complex number private: double real_part; double imag_part; J; complex number operator + (const complex number& c1, const complex number& c2) // returned: sum of c1 and c2 complex number operator- (const complex number& c1, const complex number& C2); // returned: difference of c1 and c2 complex number operator * (const complex number& c1, const complex number& c2) // returned: product of c1 and c2 complex number operator / (const complex number& c1, const complex number& c2); // precondition: c2 is not the zero of complex numbers // returned: quotient of c1 and c2 complex_number conjugate (const complex_number& c); // returned: conjugate of c double complex_modulus (const complex_number& c); // returned: modulus of c double get_imag_part () const; // returned: imaginary part of complex number private: double real part; double imag part: 1; complex number operator+ (const complex number& c1, const complex number& c2); // returned: sum of c1 and c2 complex_number operator - (const complex_number& c1, const complex_number& c2); returned : difference of c1 and c2 complex number operator * const complex number& c1, const complex number& c2); returned: product of c1 and c2 complex number operator / (const complex number& c1, const complex number& c2) /7 precondition: C2 1s not the zero of complex numbers // returned: quotient of c1 and c2 complex number conjugate (const complex number& c); // returned: conjugate of c double complex modulus (const complex number& c): /returned: modulus of c bool operator(const complex_number& c1, const complex_number& c2); // returned whether c1 and c2 are equal to each other bool operator != (const complex number& c1, const complex number& c2); // returned whether c1 and c2 are not equal to each other std: :ostream& operator