Using dynamic programming is one way to speed up the computation of Fibonacci numbers, but another is to use different algorithms. A more efficient algorithm is based on the following identities.

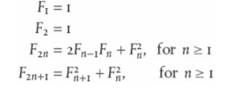
Program a function to generate Fibonacci numbers using these identities.

You can still speed up the code for generating Fibonacci numbers in the previous exercise by using dynamic programming. Do so, and construct tables like those in this section, giving the number of additions performed by the two programs.

F = 1 F = 1 F2n = 2F-1F +F, F2n+1 =F+1+F for n 1 for n 21